The Circle Story

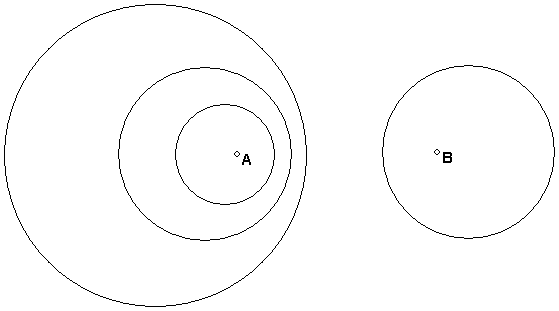
Apollonian circles are defined by ratio of distances = constant.  This means that the line AB intersects an Apollonian circle in points C and D that divide AB harmonically (just the definition of harmonic division. CD is a diameter of the circle.

Inversion of a point in at circle is intimately related to orthogonality of circles.  If P is inverted in circle c to get P', then any circle d through P and P' is orthogonal to c.

A calculation shows that inversion is related to harmonic division.  The line through the P and the circle center cuts the circle at points A and B.  Then P and P' divide AB harmonically.

Putting this all together we get important relations:

• Every circle (and line) through AB is orthogonal to every Apollonian circle of A and B (including the perpendicular bisector of AB as a circle also).
• For every point P distinct from A and B, there is exactly one Apollonian circle of A and B through C and exactly one circle through A, B, and C (including the two lines as circles as explained above).

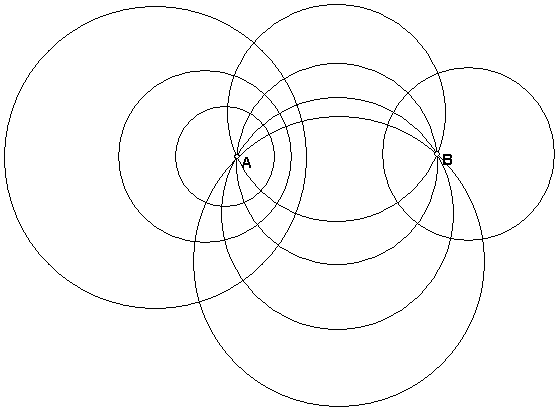
We call the set of all circles through A and B (including line AB) the elliptic pencil of circles through A and B.  We call the set of all Apollonian circles (including the perpendicular bisector of AB) the hyperbolic pencil defined by A and B. The set of all circles orthogonal to the circles of an elliptic pencil is a hyperbolic pencil, and vice versa.

If A and B get very close we get close to a limiting case, called a parabolic pencil.  These are a set of circles through A and all tangent to the same line at A (the pencil includes the tangent line.  The set of all circles orthogonal to the circles of a parabolic pencil is a parabolic pencil.

The Constructions we have learned

1. Use inversion to construct circles through P orthogonal to other circles.
2. Use the radical axis of two circles to locate the center of a circle orthogonal to two circles.
3. In the stereographic map of spherical geometry, construct the antipodal point of P by inverting in the equator circle and then rotating by 180 degrees about the center of the equator.  Images of great circles are the circles that pass through a point and its antipodal point.

The models

In the figure above with the two pencils, tell how the same constructions have different meaning in different models.