Assignment Due Wed 1/16
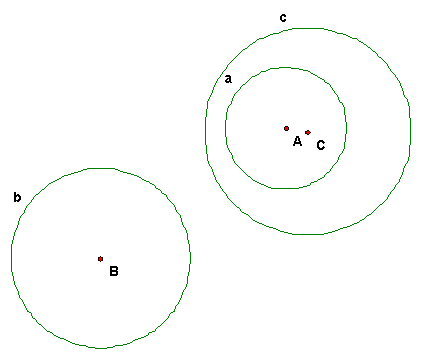
- Given 3 circles a, b, c, there are 3 radical axes of pairs of these circles.
Prove that these radical axes are concurrent except for some special cases.
Write carefully what happens in the special cases and prove the concurrence
for the other cases. Hint: The proof is almost word-for-word the same as
the proof of perpendicular bisectors of the sides of a triangle in 444, so
review that argument.
- Explain why the radical axis of two intersecting circles is the common chord
extended (i.e., the line through the points of intersection) if the circles
intersect at two points and the common tangent if the circles intersect at
one point.
- Combine 1 and 2 to give a clever shortcut for finding the radical axis of
two non-intersecting circles a and b. Let m be a circle intersecting a in
two points A1 and A2 and b in two points B1 and B2. Let P be the intersection
of line A1A2 and line B1B2. Explain why P is on the radical axis of a and
b. Then you can construct the radical axis either by constructing the line
through P perpendicular to the line of centers of circles a and b, or else
construct another point Q on the radical axis by the same method. Then the
radical axis is line PQ. Explain why this works. Then carry out this
construction in an example.
- Do all the constructions in the next section. Either use these figures
or a close copy, or do the constructions with Sketchpad and save the files
to show in lab.
Constructing Circles through Points and Orthogonal to Circles
Case 0. Construct a circle through these 3 points:

Case 1: Construct a circle through A and B and orthogonal to circle c.
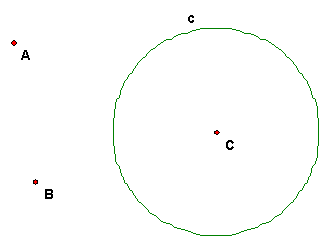
Case 2: Construct a circle through A and orthogonal to circles b and c.
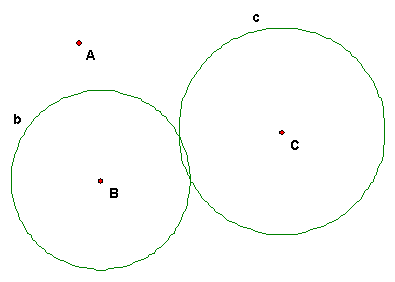
Case 3. Construct a circle orthogonal to circles a, b, c.
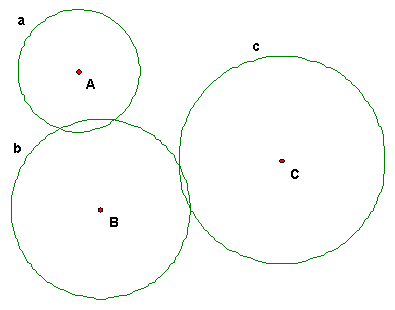
Case 3 Variant 1. Construct a circle orthogonal to circles a, b, c.

Case 3 Variant 2. Construct a circle orthogonal to circles a, b, c.