Two circle relationships
Two circle figures were used to prove Pascal's theorem and a theorem about the polar.
Pascal's theorem
Our proof of Pascal's Theorem depended on proving two triangles have corresponding sides parallel and hence (by Desargues) were perspective from a point.
The key tool for this proof was the following proposition.
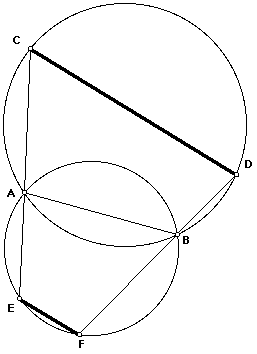
Proposition. Let two circles intersect in points A and B. If C and D are on the first circle and E and F are on the second circle and and A is on line CE and B is on line DF, then the lines CD and EF are parallel.
One figure illustrating this proposition is this:

A second one is this:
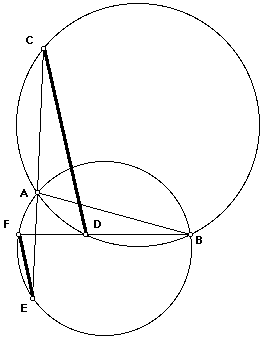
Hints for proof
Method 1: Show the lines are parallel using angles and transversals. Since ABCD are on a circle, then angles CDB and CAB are either equal or supplementary. A similar relationship in the second circle proves the lines have a transversal (for example, DF) with the required angles to prove parallelism.
Method 2: Let O be the intersection of CE and DF. Compute the power of O with respect to each circle using the two secants CE and DF. Show that triangle OCD is similar to triangle OEF.
Harmonic division and Polars
Given a circle c1 with center O and a point P, let P' be the inversion of P in c1. Construct the line p through P' perpendicular to line OP; p is called the polar of P with respect to the circle.
Theorem: Given a circle c1 and a point P, let p be the polar of P with respect to the circle. If a line m through P intersects circle c1 in points A and B, let the point Q be the intersection of m and the polar p of P. Then P and Q divide AB harmonically.
Hint for Proof: Construct the circle c2 through P, Q and P', the inversion of P in c1.
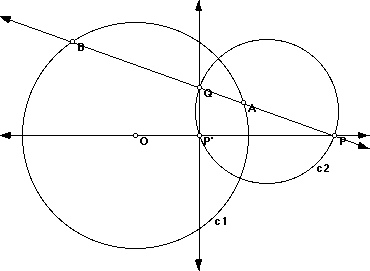
To complete the proof, discuss the following points.