NAME: ANSWER KEY

Math 444 Semi-Quiz B

Question 1: Fundamental Theorem 3 proves that every isometry of the plane is one of several types of isometry. List all the names of the types of isometry in this theorem:

See names in table below.

If you did not include them in your list, also add Identity and Point Reflection to your list to make a (possibly) longer list.

Question 2: From your longer list from Question 1, write the name of each type of isometry in one of these two columns to indicate whether it is orientation-preserving or orientation reversing.

orientation-preserving (all isometries that are a product of an EVEN number of line reflections; it is always possible to reduce the number to 2 line reflections)	orientation reversing (all isometries that are a product of an ODD number of line reflections; it is always possible to reduce the number to 1 or 3 line reflections)
Translations Rotations Identity Point Reflection (same as Halfturn – this is a special case of a rotation)	Line Reflections Glide Reflections

Question 3: In each case, write the name(s) of all the possible types that the product isometry can be. Suppose that F and G are glide reflections, L and M are line reflections, S and R are rotations.

a) What type of isometry can MR be? Line Reflection or Glide Reflection

b) What type of isometry can FG be? Translation, Rotation, Identity or Point Reflection

c) What type of isometry can LSM be? Translation, Rotation, Identity or Point Reflection

d) What type of isometry can LML be? Line Reflection (glide reflection not possible because lines are concurrent or parallel)

NOTE: The product in (a) has (1 + 2) line reflections and in (d) it has (1 + 1 + 1) line reflections, so the only possible answers are in the right column of the table above because 3 is an ODD NUMBER.

The product in (b) has (3+3) = 6 line reflections and in (c) it has (1 + 2 + 1) = 4 line reflections, so the only possible answers are in the left column of the table above because 6 and 4 are EVEN NUMBERS.

Question 4: Let m, n, p, q be 4 lines; denote the reflections in the line by R_m, R_n, R_p, R_q.

Solve this equation of isometry products to write R_q as a product of the others.

R_m R_q R_n = R_p

Multiply on the left on both sides: R_m R_m R_q R_n = R_m R_p

Since R_m R_m is the identity, R_q R_n= R_m R_p

Multiply on the right on both sides: R_q R_n R_n = R_m R_p R_n

Since R_m R_m is the identity, we get the answer:

R_q = R_m R_p R_n

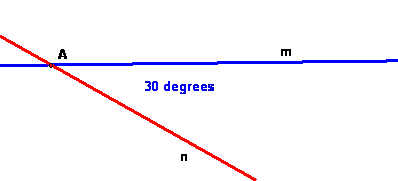
Question 5: In the figure, point A is on line m. Construct a line n so that R_mR_n = A₆₀.

(Notation: R_m and R_n are reflections in lines m and n. A₆₀ denotes rotation with center A and angle 60 degrees.)

The line n should be through A. The measure of the angle at A between m and n should be 60/2 = 30 degrees.

But there is only one possible n and there are two such lines! ORDER IS CRITICAL! The angle is measured counterclockwise from the first mirror line to the second. Since n is the first reflection, the line m is obtained by rotating n by 30 degrees COUNTER-CLOCKWISE, so n is obtained from m by rotating -30 degrees, or 30 degrees clockwise.

The other line is just wrong. For this n, the product R_mR_n = A₃₀₀.