Math 487 Lab 8 - Recognizing and Combining Isometries

Part A. Exploring Halfturns (Point Reflections)

Halfturns (also called Point Reflections) are rotations, but special ones because they are so simple. We see how they are related to midpoints, how they combine, and how they are produced as double reflections.

Experiment A1. Image of 2 points.

• In a new sketch, draw 3 points A, B, C with the point tool. Then mark A as a center.
• Rotate B and C by 180 degrees with center A. Now construct segments to form triangle ABC and triangle AB’C’.

• Drag points B and C at will and observe how the distances |BC| and |B’C’| are related. (You can measure them if you like.) How could you use triangle congruence to prove this relationship?
• Also, observe that segment BC is always parallel to segment B’C’. How can this be proved?

Experiment A2. Composition of Halfturns

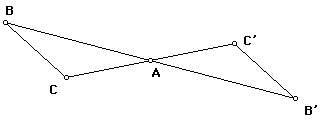
You have seen this figure before. It could be a midsegment of triangle ABC. It could also show the dilatoin of segment AB with center C' and ratio 2. But now we have another interpretation.

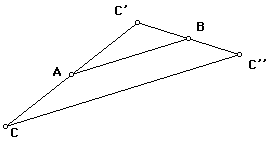
Create the figure in this way. Draw points A, B, C and segment AB. Construct C' as the image of C by the halfturn with center A and then construct C'' as the image of C' by the halfturn with center B.

Drag C around while leaving A and B fixed. Notice that the distance CC'' is constant and the segment CC'' is parallel to AB and twice as long. Therefore, if we let T(C) = C'', T is an isometry. What kind?

Then if we denote the halfturns by HA and HB, then C' = HA(C) and C'' = HB(C'). So C'' = T(C), where T is the product of halfturns. WHAT IS THE PRODUCT?

One of the powerful concepts about transformations is the concept of composition. We can get some interesting geometric figures by composing point reflections.

1. In the figure above, delete all the segments. Also, COLOR POINT C' BLUE. Then Select All and Make a New Tool called 2HT. Note the order of inputs in the Script Window.
2. In a new sketch, draw two points A and B and then draw a shape S as a polygon interior. Any irregular shape will do.



3. Now use your tool 2HT by clicking on A, B and the shape to get an S' and an S''. Then use the tool again -- click on A, then B then on S'' to get S''' and S''''. Continue to apply the tool to S''''.
4. Now start again with S and use the tool by clicking on B first and then A.
5. Observe the pattern you get as you drag S or as you drag A or B. In particular, observe that some shapes appear to be translations of each other and some not. How are the shapes spaced? Is there any consistency as you drag S?

Translations can be produced as the product of two line reflections in parallel lines or as the product of two halfturns. It can be convenient to choose one or the other in particular applications.

Experiment A4. Halfturn as a double line reflection

In a new sketch, construct two perpendicular lines m and n through a point O. The draw a point P in the plane. Reflect P in m to get P' and then reflect P' in n to get P''. Construct segments to form triangle PP'P''.

1. What kind of triangle is PP'P''?
2. How is the point O related to the sides of the triangle? Why?
3. How are the distances OP, OP', OP'' related? Why?
4. Is P'' a halfturn image of P? How does this related to the general double line reflection theorem about rotations, where the angle of the rotation is the double of the angle between the lines?
5. Repeat the same construction with P but this time reflect P across n first, then m. Do you end up in the same place? Explain.