Math 444 Quiz 2
- Part A: Answer all 4 questions in Part
A.
- Part B: Answer ONE of 3 questions 5A,
5B, or 5C. Notice 5A and 5B count more
points than 5C, so one of them is a better choice if the answer is
correct.
Part A
Problem 1 (20 points) Composition of functions
In each case, tell what kind of isometry the product could be as precisely as you can from the given information. Write ALL possible kinds but do not include kinds that you can exclude with the given information. The answers should be taken from the list of names of the types of isometries of the plane.
Answers below are in blue. (Additional explanatory
comments, not expected in student answers, are in parentheses in red.)
a) If S is a glide reflection and T is a rotation, what kind of isometry is ST?
ST is either a glide reflection or
a line reflection.
b) If U is a point reflection and V is a translation, what kind of isometry is UV?
UV is a point reflection.
(The answer "rotation"
will be counted partly right, since it is correct but not as precise as
possible.)
c) If E and F are glide reflections, what kind of isometry is EF?
EF is a rotation or translation.
(This includes the identity, but you
can list identity separately also. EF is
a rotation if the invariant lines of the glide reflections are not parallel and
is a translation if they are parallel.)
d) If A is a rotation and B is a line reflection, what kind of isometry is AB?
Glide reflection or line
reflection.
(Glide reflection if A is not on the
mirror line of B; line reflection if A is on the mirror line of B.)
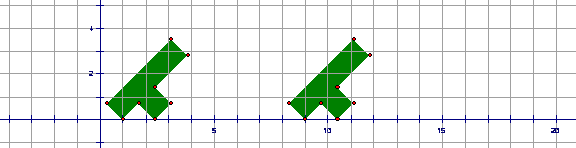
Problem 2 (10 points) Write the equations of two lines u and v so that RvRu maps the shape on the left to the shape on the right. (Notation: Ru means reflection in line u.)
The isometry that that moves the shapes is translation by 8 units horizontally to the right.
One answer: Equation for u is x =
0. Equation for v is x = 4.
Other Answers: For any choice of
constant c there is a correct answer with u equation being x = c and v equation
being x = c+4.
Problem 3 (25 points) Image of an angle
a) Write the definition of isometry.
An isometry is a transformation
that preserves distance.
b) Let T be an isometry. Suppose A, B, C be non-collinear points, and A' = T(A), B' = T(B), C' = T(C). Prove that the angles ABC and A'B'C' are congruent.
Note: You can use the definition of isometry and facts about figures in the plane, but no other theorems about isometries without proving them.
Since T is an isometry, by
definition the distances AB = A'B', BC = B'C', CA = C'A'. Therefore, by SSS, triangle ABC is congruent
to triangle A'B'C'. By corresponding
parts, then angle ABC is congruent to angle A'B'C'.
Problem 4 (20 points) Constructing defining data of an isometry
The two triangles in the figure are congruent.
Label the vertices of the second
triangle A'B'C' corresponding to the vertices of the congruent triangle ABC (you
can figure out the congruent angles in this example by inspection).
a) Tell what kind of isometry T will map triangle ABC to the other triangle.
T is a rotation with center D and
angle BDB'.
b) Construct with straightedge and compass the geometrical defining data for this isometry T.
D is the intersection of any two of
the perpendicular bisectors of AA', BB' and CC'. These perpendicular bisectors are concurrent,
so this confirms that the isometry is a rotation (in addition to the
visualization that one can do informally).
Then any of these angles is the
angle of rotation: angles
c) Make clear from labeling or comments what your method is and what the data are, but you do not have to justify your method.
Defining Data: D and angle BDB' as
described above. (Angle BDB' is shown in
yellow. It is actually 130 degrees, but
there was no way of finding this numerical measure on the quiz.)

Part B.
Answer ONE of
Problems 5A (25 points) or 5B (25 points) or 5C (15 points). You can only count one. Cross out the others if you work on more than
one
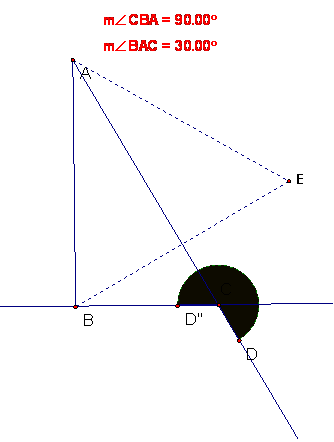
Problem 5A (25 points) Composition of rotations
Given the points A and B below; let S be rotation with center A by 60 degrees and let T be rotation with center B by 180 degrees.
a) Tell what is the isometry U = ST. Be as explicit as you can.
U is a rotation by 240 degrees with
center C constructed below.
b) Construct the geometric data defining U.
Since 180/2 = 90 and 60/2 = 30, one
must construct lines making angles of 90 degrees at B and 30 degrees at A. Then C is the intersection of these lines and
U is EF, where F is reflection in line BC and E is reflection in line AC (see
Brown, p. 69). The angle between the
lines is 120 degrees, so the rotation is by angle 240
degrees. (This
is illustrated in the figure by the sector from D to D''. It was not something that was necessary to
answer the problem on the quiz.)
The angle of 30 degrees can be
constructed by bisecting an angle of 60 degrees, which is constructed by
constructing an equilateral triangle (BAE in the figure below).
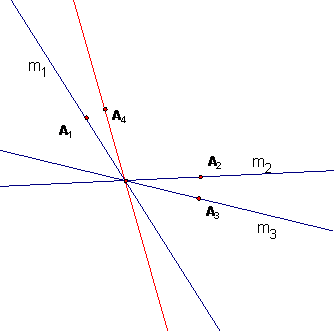
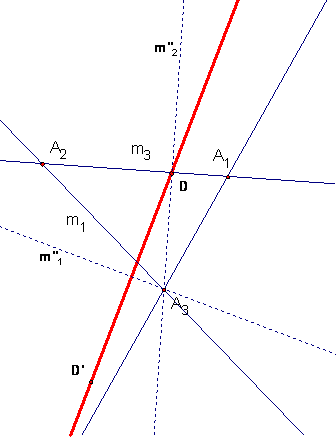
Problem 5B (25 points) Let M1, M2, M3 be line reflections in the lines m1, m2, m3 below. Let N = M1 M2 M3.
a) Tell what isometry is N. Be as explicit as you can.
N is a glide reflection. The invariant (special) line of N is the line
through the feet of the altitudes through A1 and A3.
b) Construct the geometric data defining N.
Here are 3 solutions. The first two solutions are based on the idea
of mirror adjustment as in Problem 19, page 54.
This is a proof that reflection in 3 lines, not concurrent or parallel,
is always a glide reflection.
The third solution is short because
it assumes this theorem and so begins with the knowledge that N is a glide
reflection.
Solution 1
Construct the altitude through A1
and call this line m2'. Let C
be the foot of this altitude.
Then construct m3' so
that M2'M3' = M2M3 (denoting
reflection in m2' and m3' by M2' and M3'). In effect this means that one applies mirror
adjustment and rotates line m3 by angle A2A1C so that the
angle from m2' to m3' is the same as from m2
to m3.
Then N = M1(M2
M3) = M1(M2'M3') = (M1M2')M3'
= C180 M3'.
This uses the observation that double
reflection in the perpendicular lines (M1M2') is a rotation
by 180 degrees with center at C, i.e., a point symmetry with center C.
But in an assignment it was shown
that a line reflection followed by a point symmetry is a glide reflection
with special line g = line through C perpendicular to m3'.
Let C' be
the reflection of C in m3'. Then
N(C') = C180 M3'(C') = C180 (C) = C.
So the glide vector of N is C'C.
So N is a glide reflection with invariant line CC' and glide
vector C'C. Thus N = GC'C in our usual glide reflection notation.
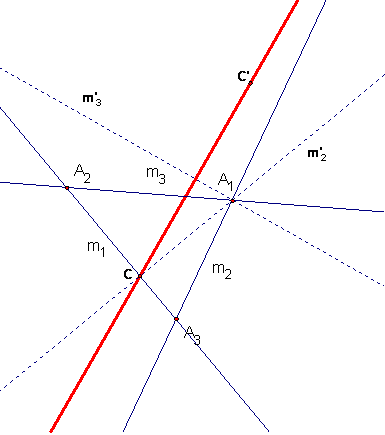
Solution 2
This is very much like Solution 1
except that one constructs the altitude m2" through A3
and then m1" through A3 so that M1"M2"
= M1M2 (M1" and M2" being
the reflections in lines m1" and m2").
Let D be the foot of the altitude
so that the perpendicular lines m3 and m2" intersect at D.
Then as before N = (M1M2)
M3 = (M1"M2") M3 = M1"(M2"M3)
= M1"D180.
This is a glide reflection with
invariant (special) line g through D perpendicular to m1".
If D' is defined as M1"(D),
then N(D) = M1"D180 (D) = M1"
(D) = D'.
So N is a glide reflection with invariant line DD' and glide
vector DD'. Thus N = GDD' in our usual glide reflection notation.
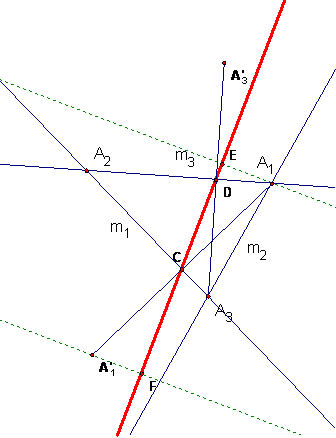
Solution 3
This solution is based on already
knowing that N is a glide reflection and then solving for the invariant line by
finding images of two points and then constructing the midpoints.
Let A1' be the
reflection of A1 in line m1 and let A3' be the
reflection of A3 in line m3. Then since A1 is on both lines m3
and m2,
N(A1) = M1(M2(M3(A1)))
= M1(M2(A1)) = M1(A1) =
A1'.
Similarly N(A3')
= M1(M2(M3(A3'))) = M1(M2(A3))
= M1(A3) = A3.
Let C be the midpoint of A1A1'
and let D be the midpoint of A3A3'.
Then the invariant (special) line g
of N passes through these midpoints.
Notice that as before, C and D are the feel of
two altitudes, so this is the same line as before (as it must be).
A glide vector of N can be found by
constructing perpendicular lines to g through A1 and its N image
A1'. If the feet of these perpendiculars are E and
F, then EF is a glide vector for N.
So N is a glide reflection with invariant line DC and a glide
vector of N is EF. Thus N = GEF in our usual glide reflection notation.
Problem 5C (15 points) Let M1, M2, M3 be line reflections in the lines m1, m2, m3 below. Let N = M1 M2 M3.
a) Tell what isometry is N. Be as explicit as you can.
Since N = M1 M2 M3
for concurrent lines, then N is a line reflection.
Since N = M1 M2 M3,
then
b) Construct the geometric data defining N.
Label as O the point of concurrence
of the lines. Drawing points A1,
A2, A3 on the lines in the figure, construct a point A4
on N by copying angles so that angle A2OA1 = A3OA4.