Theorem (3 point theorem, AKA 3 thumbtack theorem)

Suppose that F and G are isometries of the plane and that ABC is a triangle.

If, F(A) = G(A) = A', F(B) = G(B) = B' and F(C) = G(C) = C', then for all points P, F(P) = G(P).  In other words, F = G.

Proof:

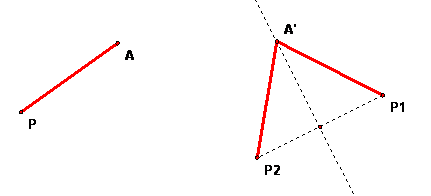
Suppose there is a point P so that F(P) = P1 and G(P) = P2 but P1 is not equal to P2.

Then

1. |A'P1| = |A'P2|. 

• Why?   |A'P1| = |F(A)F(P)| since A' = F(A), and this = |AP|, since F is an isometry.  Likewise, |A'P2| = |G(A)G(P)| = |AP|.

• What is the picture?  Since A'P1| = |A'P2| = |AP|, the segment AP is mapped by F to one segment with endpoint A' and by G to another segment with endpoint A'; both segments are congruent to AP, so A' is on the perpendicular bisector of P1P2.

2. |B'P1| = |B'P2|.  Why?  What is the picture?

• For the same reasons, |B'P1| = |B'P2| = |BP| and B' is on the perpendicular bisector of P1P2.

3. |C'P1| = |C'P2|.  Why?  What is the picture?

• For the same reasons, |C'P1| = |C'P2| = |CP| and C' is on the perpendicular bisector of P1P2.

This is a contradiction to the assumption that P1 is not P2.  Putting all 3 results together means all 3 points A', B', C' are on the perpendicular bisector of P1P2.

In particular, A', B', C' are collinear.  But we assumed at the outset that ABC was a triangle.  By SSS, then A'B'C' is a congruent triangle and the points cannot be collinear.

This is a contradiction.  The only way out of the contradiction is to conclude is we cannot choose a point P so that P1 is not equal to P2.   So F(P) = G(P) for all p.

Another way to say the same thing:  Given 3 points A, B, C.  Denote the distances between points by a = |BC|, b = |CA|, c = |AB|.  Since F and G are isometries, also a = |B'C'|, b = |C'A'|, c = |A'B'|.  One of the 3 distances is greater than or equal to each of the others.  Assume this longest side is c.  If A, B, C form a triangle, a + b > c by the triangle inequality.  If A, B, C are collinear, then a + b = c by addition of segments on a line.  So we started with a triangle ABC satisfying the inequality and ended up with the equality, which is a contradiction.