Ratios in Triangles and Trapezoids

Part 1: Find equal ratios | Part 2: Find answers for r = 7/13 | Part 3: Find answers for general r

Answer to problem 6.3

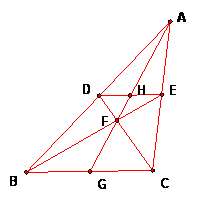
Suppose that DE is parallel to BC and AE/AC = 7/13.:

a)      What is the ratio BF/FE?

b)      What is the ratio BF/BE?

c)      What is the ratio AF/AG?

Part 1:  Find some equal ratios from similar triangles.

Since DE is parallel to BC, there are lots of angles that are equal because they are cut by transversals, and this leads to many pairs of similar triangles.  Here we point out triangles that are similar by the AA criterion.  We leave it to the reader to fill in the equal angles from transversals.

GOAL: To show that AH/AG = 7/13 and FH/FG = 7/13.

Note:  We will state some theorems about transversals and about dilations what will make these steps much shorter in a later version of this answer.

Step A. Triangle AED is similar to triangle ACB.

Therefore, AD/AB = DE/BC = AE/AC = 7/13.

Step B. Triangle AEH is similar to triangle ACG.

Therefore AH/AG = HE/GC = AE/AC = 7/13.

Thus AH/AG = 7/13.

Step C. Triangle FED is similar to triangle FBC.

Therefore FE/FB = FD/FC = DE/CB = 7/13. (by Part A)

Step D. Triangle FHE is similar to triangle FGB.

Therefore FH/FG = EH/BG = FE/FB = 7/13. (by Part C).

Thus FH/FG = 7/13.

 

Part 2: Finding the ratios in the problem

From Part 1 we see the following ratios (details in the calculations below).

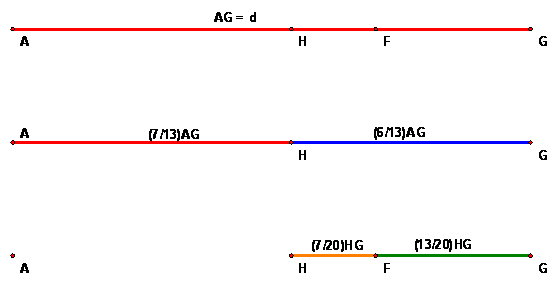
The answer will turn out to be simpler than one might think:

DETAILS:  Several computations to get this answer.

a)      What is the ratio BF/FE?

We see in Step D above that BF/FE = FB/FE = 13/7.

b)      What is the ratio BF/BE?

We can see the ratio a couple of ways.  One way is to use addition of segments.

Since FE/FB = 7/13, BE = BF + FE = BF + (7/13)BF = (20/13)BF.

Thus BF/BE = BF/((20/13)BF) = 13/20.

A second way of expressing the same thing is to introduce a dummy variable x.

BF = 13 x, and FE = 7x.  Then BE = 20x.  So BF/BE = 13x/20x. = 13/20.

c)      What is the ratio AF/AG?

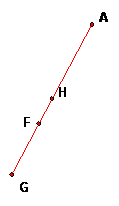
We have 4 points on a line.  We know that AH/AG = 7/13 and that FH/FG = 7/13 also.

Again, we can do the computation with or without a dummy variable.  Also, there is a SHORTCUT outlined below.

Method 1

AH + HG = AG, so HG = AG - AH = (1 – 7/13) AG = (6/13)AG.

Since FG/HF = 13/7, FG = (13/7)HF.  Thus HG = HF + FG = (1 + (13/7)HF = (20/7)HF.

Therefore, HF = (7/20)HG = (7/20)(6/13)AG.

Finally, AF = AH + HF = (7/13)AG + (7/20)(6/13)AG = (7/13)( 1 + (6/20))AG = (7/13)(13/10)AG = (7/10)AG.

Thus AF/AG = 7/10.

Shortcut:  Compute FG/AG and subtract:  AF/AG = 1 – (FG/AG).

It is easier to compute FG, since no addition step is necessary.

HF = (7/13)FG, so  HG = (7/13)FG + FG = (20/13)FG.  Thus FG = (13/20)HG = (13/20)(6/13)AG = (3/10)AG.

Method 2

Sine AH/AG = 7/13. let AH = 7x and so AG = 13 x.  Then HG = 13x – 7x = 6x.

Also, FG/HF = 13/7, so let FG = 13y and HF = 7y.  Then HG = 13y + 7 y = 20y.

So we have HG = 6x = 20 y.  Thus y = (3/10)x and HF = 7y = (21/10)x.

Thus AF = AH + HF = 7x + (21/10)x =(7*13/10)x.

Since AG = 13 x, AF/AG = (7*13/10)x/13x = 7/10.

Again, AF/AG = 7/10.

Shortcut: Compute FG and subtract.

HG = 6x.  FG/HG = 13y/20y = 13/20, so FG = (13/20)6x = (3/10)13x

AF = AG – FG = 13x(1 – (3/10)) = 13x(7/10) 

AF/AG = (7/10)13x/13x = 7/10.

Part 3: Answer to GENERALIZED problem 6.3

Suppose that DE is parallel to BC and AE/AC = r.

a)      What is the ratio BF/FE?

b)      What is the ratio BF/BE?

c)      What is the ratio AF/AG?

Part 1:  Find some equal ratios from similar triangles.

Since DE is parallel to BC, there are lots of angles that are equal because they are cut by transversals, and this leads to many pairs of similar triangles.  Here we point out triangles that are similar by the AA criterion.  We leave it to the reader to fill in the equal angles from transversals.

GOAL: To show that AH/AG = r and FH/FG = r.

Note:  We will state some theorems about transversals and about dilations what will make these steps much shorter in a later version of this answer.

Step A. Triangle AED is similar to triangle ACB.

Therefore, AD/AB = DE/BC = AE/AC = r.

Step B. Triangle AEH is similar to triangle ACG.

Therefore AH/AG = HE/GC = AE/AC = r.

Thus AH/AG = r.

Step C. Triangle FED is similar to triangle FBC.

Therefore FE/FB = FD/FC = DE/CB = r. (by Part A)

Step D. Triangle FHE is similar to triangle FGB.

Therefore FH/FG = EH/BG = FE/FB = r. (by Part C).

Thus FH/FG = r.

 

Part 2: Finding the ratios in the problem.

a)      What is the ratio BF/FE?

We see in Step D above that BF/FE = FB/FE = r.

b)      What is the ratio BF/BE?

We can see the ratio a couple of ways.  One way is to use addition of segments.

Since FE/FB = r, BE = BF + FE = BF + rBF = (1+r)BF.

Thus BF/BE = BF/((1+r)BE) = 1/(1+r).

A second way of expressing the same thing is to introduce a dummy variable u.

BF = u, and FE = ru.  Then BE = (1+r)u.  So BF/BE = 1/(1+r).

c)      What is the ratio AF/AG?

We have 4 points on a line.  We know that AH/AG = r and that FH/FG = r also.

Again, we can do whit with or without a dummy variable.

Method 1

AH + HG = AG, so HG = AG - AH = (1 – r) AG = (1 - r)AG.

Also, HG = FG + FH = (1/r)FH + FH = (1 + (1/r))FH = ((r+1)/r)FH.

Thus (1-r)AG = HG = ((r+1)/r)FH.

So FH =(r(1-r)/(1+r))AG.

Finally AF = AH + FH = rAG + (r(1-r)/(1+r))AG = (1 + (1-r)/(1+r)) r AG =

 (2r/1+r))AG, since (1+r + 1 – r)/(1+r) = 2/(1+r).

Thus AF/AG = 2r/(1+r).

Method 2

Since AH/AG = r. let AH = rx and so AG = x.  Then HG = x – rx = (1-r)x.

Also, HF/FG = r, so HF = rFG.

So let FG = y and HF = ry.  Then HG = y + r y = (1+r)y.

So we have HG = (1-r)x = (1+r)y.  Thus y = ((1-r)/(1+r))x and HF = ry = r((1-r)/(1+r))x.

Thus AF = AH + HF = rx +  r((1-r)/(1+r))x = rx(1 + (1-r)/(1+r)) = 2rx/(1+r).

Since AG = x,, AF/AG = 2r/(1+r).

Shortcut: Compute FG and subtract.

HG = (1-r)x.

FH = rFG.

HG = FG + FH = (1+r)FG.

FG = (1/(1+r)HG = ((1-r)/(1+r))x.

AF = AG – FG = x - ((1-r)/(1+r))x = x((1+r) – (1-r))/(1+r) = x(2r/(1+r).

AF/AG = x(2r/(1+r)x = 2r/(1+r).