In-Class Work: Friday, October 15, 2004

The "surfer problem"

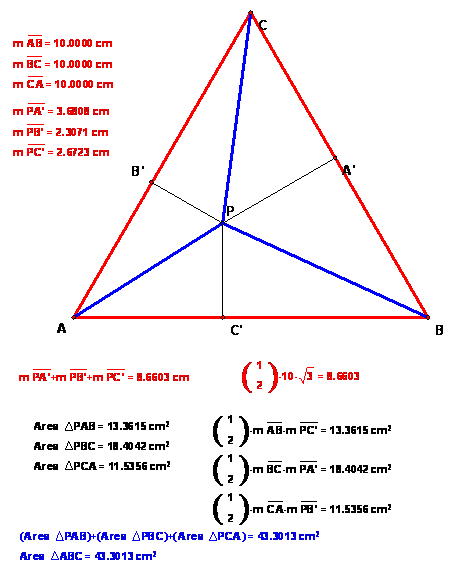
The name of this problem is taken from an excellent secondary textbook, Geometry, by Harold Jacobs. This book begins with a problem called the Surfer and the Spotter. This is adapted from one of the two questions in that book: There isan island in the shape of an equilateral triangle; each side of the triangle is a good surfing beach. A surfer is living on the island and wants to visit each side of the island to surf, so she decides to site her thatched-roof hut at a point where the sum of the distances to each of the 3 beaches is a minimum. Where should the hut be?

Goals for the activity

What one can bring away from this problem includes the following. (1) height and area of an equilateral triangle from the Pythagorean theorem -- important standard example (2) both the positive and negative sides of accuracy in geometry measuring experiments (3) problem solving using area and decomposition of a figure.

Modeling the problem as a class activity

• Draw a segment AB of length 10 cm; then construct an equilateral triangle ABC with AB as one side.
• Draw a point P somewhere in the triangle. Students should make their own choice, so there will be a good quantity of independent data.
• Construct a point A' on BC, B' on CA, C' on AB so that PA' is perpendicular to BC.  And likewise PB' and PC' are perpendicular to CA and AB, respectively.

• Measure the 3 lengths of the segments and find the sum.  What is your answer?

Answers and References

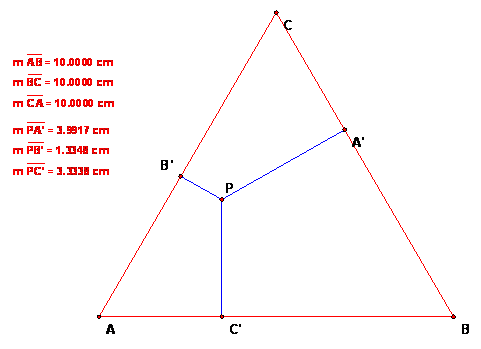
Students found that all their answers were close, though the answers ranged from about 8.5 to 9.1. So either the sums are different but close, or they are all the same and the differences result from experimental error.

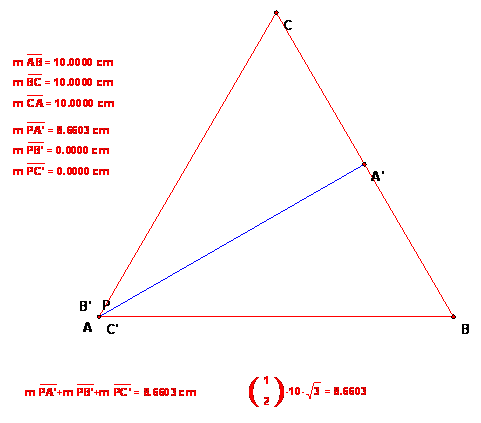
If the sums are really always the same, then any point P will give the same value, including the special case where P = A, as in this figure. In this case, two lengths = 0 and the other length = the height of the triangle, which is 10*(1/2)sqrt 3 by the Pythagorean theorem. This number is about 8.66, which is close the most popular experimental values.

So conjecturing that the sum is constant, we know the exact value of the sum. But we don't have a reason yet for being sure that the sums are really constant. That comes from the next step. Divide triangle ABC into 3 smaller triangles, PAB, PBC, PCA. These triangles all have equal bases 10 = AB = BC = CA and the heights are PC', PA', PB'. So the areas are (1/2)*10*PC', (1/2)*10*PA', (1/2)*10*PB' and the sum of the areas is

(1/2)*10*(PC' + PA' + PB'). But this sum of areas equals the area of ABC = (1/2)* 10 * h, where h is the height of ABC. This means that h = (PC' + PA' + PB') for any choice of P. So this is the constant. As we have seen, the value of h is (1/2)*10*sqrt 3.

Note: The value of |AB| = 10 was chosen as a simple example. In the general case, if we set AB = s, then the height h = (1/2)s*sqrt 3 and this is the sum (PC' + PA' + PB').

Note about the figure: There are some displayed (1/2)'s in the figure for which the fraction bar does not appear on the web page.