This is a quick introduction to a way of implementting a glide reflection transformation with Sketchpad. There are also instructions (for later) for how to do this on paper with straightedge and compass.
This part is based on downloading a Sketchpad file and doing some experiments to show the Fundamental Theorems 1 and 2 of Isometries. (See Brown Section 1.10.)
In a new sketch, draw a line AB. We will denote line reflection in line AB by R and we will denote by T the translation by vector AB. The glide reflection GAB will be defined to be TR.
Make a tool. Hide point P' and select, A, B, the line, and points P and P''. Make a tool. Call it G_AB. The inputs to the tool should be points A and B and and "pre-image C" or something like that. So the object C to be transformed can be any object.
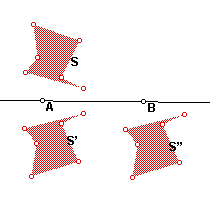
How to glide reflect a shape with SketchpadHow to glide reflect a shape with Sketchpad
OR
|
|
The transformation that takes S to S’’ is the glide reflection GAB.
Draw two points A and B and a line AB = m..
Draw a point P and construct the reflection P' of P in line m. (Drop a perpendicular to m through P and then mark off an equal distance on the opposite side of the line to get the reflection.)
Translate P' by AB to get P''. (Construct the line n through P' perpendicular to PP' and then mark off distance AB on n to get P'' so that AB = P'P''. If P is not on m, then ABP''P' is a parallelogram.)
Then P'' = G(P) for the glide reflection G = gAB, which is by definition TR, where R is reflection in m and T is translation by AB.
To construct G of a shape, image points can be constructed one by one. However, recalling that for any shape U, G(U) is congruent to U, once the image of a couple of points is constructed the rest may be constructed from information from U. For example, to construct the image of a sqaure ABCD, once one has found the images G(A) and G(B), then the rest of the image square can be constructed from these points.
This part is based on downloading a Sketchpad file and doing some experiments to show the Fundamental Theorems 1 and 2 of Isometries. (See Brown Section 1.10.)
To help visualize a transformation T, one method is just to look at a shape like a triangle or a letter of the alphabet and then look at the image. This is actually enough to tell everything about T, if T is an isometry, as we saw in Part B. However, while may be true logically, some additional clues can help.
One way is start with a shape S and then find not only the image T(S), but also the image of the image T(T(S)), denoted T2(S), and then T3(S), and so on. In principle we can do this for all possible n, both positive and negative. In practice, a few steps tells a lot.
This collection of images is called the T-orbit of S, or informally the T-footprints of S.
Draw a line AB and a point P not on line AB. Let G = GAB be the glide reflection defined above.
Suppose G is a glide reflection. With Sketchpad, it is easy to start with a shape S and then construct images G(S), G2(S), G3(S), G4(S), etc. The set of these images is part of the G-orbit of S.
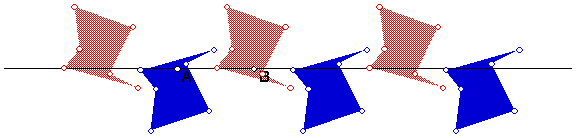
In this figure the shapes are colored differently, according to whether they = Gn(S) for even or odd n.
Draw a triangle ABC and a shape S. Reflect S across line BC to get S', reflect across CA to get S'' and reflect across AB to get S'''. Hide S' and S'' and let T(S) = S'''. Make a tool and find the T-orbit of S. Can you use this to "guess" what kind of transformation T is?
How can we visualize geometrically the square root of -3 (for example)? In this course for any real number r (and a center ) we know how to dilate by that number. Dilations compose by multiplication of the ratios r.
So if T is dilation by ratio -2 with center O, what is T2?
Here is a sketch that explores this. For extra credit, as a long-term challenge, can anyone extend this file to explain the square root of -3 geometrically?
