Rows and rows of triangles

Start with 3 points A, B, C and construct segments to form the sides of triangle ABC. Then construct a point D so that ABCD is a parallelogram.

Also construct segments CD and DA to form the other sides of the parallelogram.

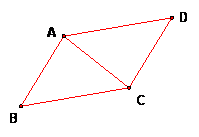
Make a tool from this construction. It will start with A, B, C and construct D and the sides of the triangle and parallelogram.

Now use the tool on some points in the figure to create a trapezoid like this:

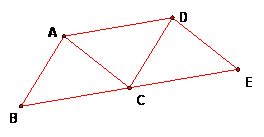
IMPORTANT: It appears that the points B, C and E are collinear. How can we prove that this is really so? What fact do we use?

If the original triangle has area T = (1/2)ah, with a = BC and h = the height. What is the area of this trapezoid? Notice there are two "upward" triangles with sides BC and CE and one "downward" triangle with side AD.

Now make a longer strip of triangles like this, using your GSP tool.

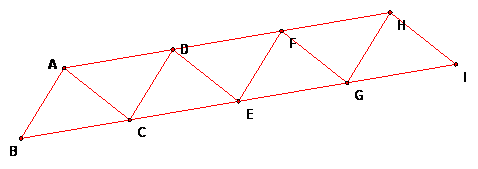
Is this still a trapezoid? What is the number of "up" triangles, what is the number of "down" triangles? What is the total number of triangles?

We call this a trapezoidal strip of size 4 because it has 4 segments in the longer of the two parallel sides.

Triangular Arrangement of Triangles

The goal of this section is to study triangles that are made up of congruent triangles using the trapezoidal strips we just constructed. Here is an example; we will call this the triangular arrangement of size 4 made from ABC.

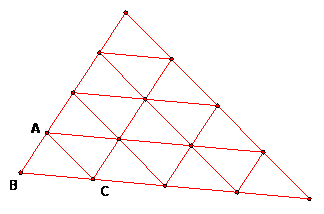
For each such triangle, we think of the triangle being built up from the previous size by adding a trapezoidal strip. For example the triangle of size 4 is formed from the triangular arrangement of size 3 plus a strip of size 4.

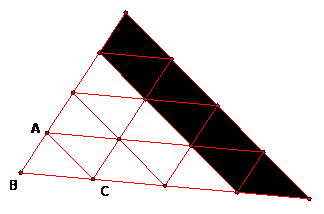
Your task in the lab is to use your GSP tool to build up triangles from size 1 to size 5, count triangles and tabulate to discover some numerical relationships.

Size = n	Number of triangles in strip of size n	Number of triangles in triangular arrangement of size n
1
2
3
4
5

You should find that the number of small triangles in the triangular arrangement of size n equals the sum of the number of triangles in each of the strips of size 1, 2, …, n. Is this true?

• What will be the number of triangles in general in a strip of size n?

• What will be the number of triangles in general in a triangular arrangement of size n?

• What formula for size n do you get by adding up the number of triangles in each strip to get the number of triangles in the triangular arrangement of size n?

Angles and Parallels

• Are all the angles in the triangular arrangement figure the same as one of the angles in the triangle ABC? Why?

• Are all the line segments drawn in a triangular arrangement figure like the one above parallel to one of the sides of ABC? Why?

• If A5 is the area of the triangle of size 5 and A3 is the area of the triangle of size 3, what is the ratio A3/A5 obtained by counting triangles?

More numbers

What is the number of "up" triangles in the triangular arrangements of size 1, 2, 3, 4, and 5.

What is the number of "down" triangles? How are the two numbers related? What is the sum of the up and the down for a given size?

Extra: Can you find the number of "up" and "down" for general n?