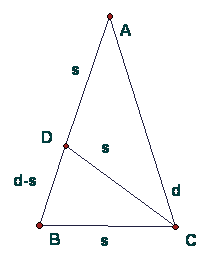
Given a triangle ABC, with D on segment AB, if AB = AC = d and CB = CD = DA = s, find the ratio d/s.
Step 1. This is the given figure, with the lengths labeled (note DB = AB - AD = d-s).

Since ABC and CBD are isosceles triangles that share a common base angle ABC = angle CBD. Since they are isosceles, the base angles are equal and angle ACB = angle ABC = angle CBD = angle CDB. Thus triangle ABC is similar to triangle CBD by AA
|
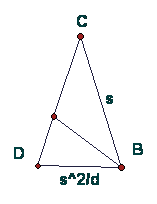
Since side AC in triangle ABC corresponds to side CD in triangle CDB, the scaling ratio from ABC to CDB is CD/AC = s/d. Therefore, since DB in the smaller triangle corresponds to CB = s in the larger triangle, the length of DB = (s/d)s = s^2/d. Another way to see this is simply by corresponding sides, DB/CB = CB/AC, so DB/s = s/d and DB = s^2/d. But since we already know DB = d-s, it must be true that d-s = s^2/d, or by clearing the denominator, d^2 - sd - s^2 = 0. Other forms of this equation could emerge from these similar triangles. For example CA/CB = BC/BD implies d/s = s/(d-s). This equation is equivalent to the other one after some cross-multiplication. |
 |
This is an equation relating d and s. Is this the answer? No. The answer is the numerical value of d/s if it can be found. Here are some methods of solution.
The problem is to solve the equation we have that involves s and d so that we have a solution of d/s. This means that we keep the goal of finding d/s in mind and look for d/s in the equation, while trying to eliminate the other variables.
If we start with d - s = s^2/d, we can collect all the variables on the left side by multiplying by d/s^2 to get d(d - s)/s^2 = 1. We group one d/s together to get (d/s)(d - s)/s = 1 and then divide the term inside parentheses to get (d/s)((d/s) - 1) = 1.
This is a quadratic equation in d/s. Collecting all the terms on the left, as usual, we have
(d/s)^2 - (d/s) - 1 = 0. By the quadratic formula we solve for d/s to get two solutions
d/s = (1 + sqrt 5)/2 and (1 + sqrt 5)/2. However only one of these roots is positive, and we know that the ratio of these positive lengths is positive, so the answer is
d/s = (1 + sqrt 5)/2
If you started with one of the other equations in s and d, such as d/s = s/(d-s), perhaps it is hard to separate out the d/s. To make this easier, give the ratio a name. Set d/s = K.
Now to introduce K into the equation, replace one of the variables by an expression in K and the other variable. For example, since d = sK, substitute this value for d everywhere.
The equation d/s = s/(d-s) becomes sK/s = s /(sK - s). But we can simplify the fraction on both sides by dividing the numerator and denominator by s, so we now have
K = 1/(K - 1). It is pretty clear what to do now; multiply by (K - 1) to get 1 = K^2 - K and then collect terms to get the quadratic equation K^2 - K - 1 = 0.
Again by the quadratic formula, K = (1 + sqrt 5)/2 or (1 + sqrt 5)/2, which has only one positive root. Since K is positive,
K = (1 + sqrt 5)/2
If we started with the form of the equation d^2 - sd - s^2 = 0, then since d = sK, s^2K^2 - s^2K - s^2 = s^2(K^2 - K - 1) = 0. Since s is not zero, we can divide by s^2 to get K^2 - K - 1 = 0 as before.
Side comment about the polynomial algebra. If we substitute d = sK, can we always factor out a power of s and get a polynomial only in K? If you are curious, try the method for the following polynomials: f(s,d) = 2d^2 + 5 sd + 3s^2, g(s,d) = d^2 + 3s^2 + d, h(s,d) = 2d + 5 s, j(s,d) = k^3 - s^3. You can factor out s and get a polynomial in K for f, h, j but not g. The reason is that each of the monomial terms must have the same total degree n. (The standard name for such a polynomial is a homogeneous polynomial of degree n.) So for f, each of the monomials has degree 2, for g each has degree 1 and for j each has degree 3. But for g, there are two monomials of degree 2 and one of degree 1. Can you see why that s^n can be factored out for a homogeneous polynomial of degree n after substituting d = sK?
Instead of jumping directly to the algebra as above, consider simplifying the triangular figure first. The problem is to find the ratio of two sides in a triangle. We will get the same ratio for corresponding sides in any similar triangle, so we can try to simplify the problem by choosing a unit and constructing a similar figure with the side corresponding to s to be = 1. Then the side corresponding to d will be d/s = K.
Here is triangle A'B'C' with point D' on A'B', it is similar to the original figure of triangle ABC with D.
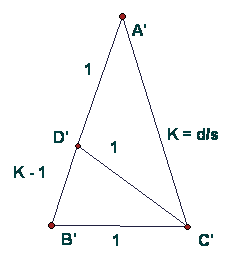
So again we note that triangle A'B'C' is similar to triangle C'B'D', so again K/1 = 1/(K-1) because A'C/C'D' = B'C'/B'D'.
But this leads immediately to K^2 - K = 1, etc., as in the previous solution.