Answers and Comments

1. Problem: A Distance

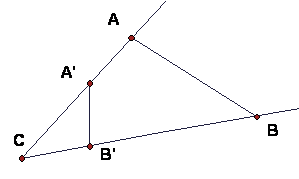
In the figure, point A' is on ray CA and point B' is on ray CB. Suppose |CA| = a and |CA'|= 6/a.  Also |CB| = 2 and |CB'| = 3.  If |A'B'| = c, what is |AB|?

Show your work and give (brief) reasons.

Answer: |AB| =   ___________

Work:

Answer: This should be viewed as a straightforward check of similarity and use of the scaling factor. If it does not seem simple, that is because (1) the triangle is flipped (2) some dimensions are given by letters and not numbers. But your understanding and technique for similar triangles should be sufficiently robust to withstand such complications.

Even though the drawing is not to scale, one suspects that if there are similar triangles in the figure, triangle ABC is similar to B'A'C and not A'B'C. So we will check that one first.

If ABC is similar to B'A'C, the scale factor from ABC to B'A'C is k = B'C/AC = A'C/BC = B'A'/AB.

But B'C/AC = 3/a and A'C/BC = (6/a)/2 = 3/a, so these ratios are equal and the triangles are similar by SAS. Then k = 3/a = B'A'/AB = c/BA, so BA = ac/3.

Errors: What went wrong?

There were two big kinds of errors on this problem, and one medium error..

1. Most disturbing were those papers that proved that triangle ABC is similar to A'B'C. This is clearly wrong on visual and inuitive grounds. The ratios of sides are not equal. The corresponding angles are not equal. Some students seemed to think that a could be anything or that it could be solved for in the equation of ratios. Not true.
2. The second common error derives from a useful fact that for SAS. From the definition of similarity, for SAS one checks B'C/AC = A'C/BC. The pattern is that one is checking two ratios of corresponding sides, b'/b = a'/a; the numerators are sides in one triangle and the denominators are sides in the other triangle. If it handy sometimes to check the equivalent equation b'/a' = b/a; in this case one is comparing an internal ratio in one triangle with the corresponding internal ratio in the other. But DANGER lurks. The ratios b'/b = a'/a = the scaling ratio, but the ratios b'/a' = b/a do NOT equal the scaling ratio, they are the ratios of the sides of a single triangle. If one gets confused and takes this ratio as the scaling ratio, then it is all wrong.
3. A third error occurs after the triangles are shown to be similar correctly. If the scaking ratio from ABC to B'A'C is k, then the scaling ratio the reverse direction is 1/k. This is another place one can make a mistake, nearly at the finish line.
   

2. Problem: Ratios in a trapezoid (25 points)

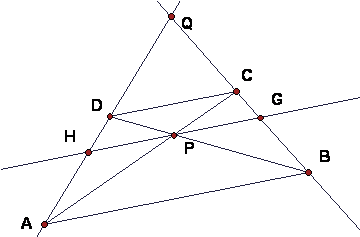
Let ABCD be a trapezoid, with side AB parallel to CD. 

Suppose that diagonal AC intersects diagonal BD at P and line BC intersects DA at Q.

Also, the line through P parallel to AB intersects BC at G and DA at H.

The length of AB = 4 and the length of CD = 1. (The figure is not to scale.)

For each question, write the answer in the blank space, but show your work below. (This is not a proof; just show how you solved it.)

(a)    Find the ratio |GC|/|GB|.  _________________

(b)   Find the ratio |QC|/|QB|.  _________________

(c)    Find the ratio |DP|/|DB|.  _________________

(d)   Find the ratio |BG|/|BQ|.  _________________

(e)    Extra: No further computation necessary if you have answered a-d: Write the barycentric coordinates of P with respect to ABQ  _________________

Answer: The answer to (a) and to (b) is 1/4. This follows from two Thales or dilation figures. The first one shows triangle QDC is similar to QAB with ratio 1/4 and the second one shows that triangle PCD is similar to triangle PAB with ratio 1/4.

(c) 1/5 is the answer. If DP = x, then DB = 4x and PD+DB = 5x = BD, so |DP|/|DB| = x/5x = 1/5

(d) 3/5 is the answer.

1. One solution method: |BG|/|BQ| = (|BG|/|BC|)(|BC|/|BQ|) = (4/5)(3/4) = 3/5.
2. A second method is to introduce some temporary units. For instance, if we set |QC| = t, then |BQ| = 4t and |BC| = |QB| - |QC| = 4t - t = 3t. Now if we see that |BG| = (4/5)|BC|, we get |BG| = (4/5)3t, so |BG|/BQ| = (12t/5)/4t) = 3/5.
3. If we prefer, we can even put in two units and then compare them. Set |QC| = t, and get |BQ| = 4t and |BC| = 3t as above. Also set CG = s, so BG = 4s. Then |BC| = 4s + s = 5s. But then on quantity can be written both in terms of t and in terms of s: |BC| = 3t = 5s, so s/t = 3/5. Then we conclude that |BG|/|BQ| = (4s)/(4t) = s/t = 3/5.

Each of these methods works. Notice that they get a little more formal and slower each time, so if you can see a ratio sooner, as in the first two methods, the answers will come quicker. But the last one is methodical and sure.

(e) (1/5, 1/5, 3/5)

The main point of this is to encourage everyone to see that this figure is really just a special case of a triangle with cevians and barycentric coordinates. So those ideas should be connected with this trapezoid figure. In this case, there is a triangle ABQ and a point P inside the triangle. Lines AP and BP are cevian lines that cut their opposite sides in the ratios 4/1 and 1/4. So the cevian QP will cut AB in ratio 1/1 by Ceva's theorem . Thus PQ intersects AB at its midpoint (this was proved independently in an assignment).

If (x,y,z) are the barycentric coordinates of P with respect to ABQ, we find that two of the ratios that have already been computed are exactly ratios that have been used to compute barycentric coordinates. For example, the ratio from (c) is a ratio on a cevian that = y = 1/5 and the ratio from (d) is a rato along a side cut by a parallel to AB through P and = z = 3/5. Since the sum must equal 1: x+y+z =1 , then x = 1/5. Notice that this fits:with the known fact that x = y because PQ intersects AB at its midpoint.