
Do all problems. Show any work that you do on the paper.
Construct with straightedge and compass a circle tangent to all 3 lines. WRITE down the main features of the construction (not every tick mark, but what the main points and lines and segments are).

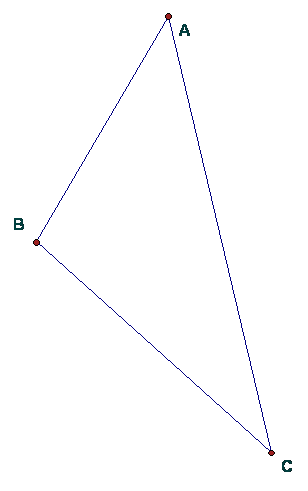
Given triangle ABC in the figure, construct the circle through points A, B, C.
What is the name given to this circle? __________________________
On a line are points A, B, C and a ruler that makes points A and B correspond to numbers a and b. If B is the midpoint of AC, what number corresponds to C? (Answer should be an expression in a and b.)
Suppose that m and n are lines that intersect at O. If P is a point equidistant from the two lines, prove that P is on a bisector of one of the angles defined by the two lines.
(You can use any of the theorems that you know to prove this, except what you
are proving, of course.)
In this figure, E is on line AC and D is on line AB, and angles ABC, ACD, and ADE are right angles. Length |AB| = 4 and |AC| = 5.
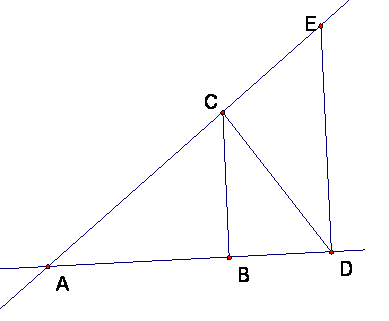
Compute an exact numerical value (i.e., not a decimal approximation) for the lengths of the following segments. Show your reasoning clearly enough to follow, but THIS DOES NOT HAVE TO BE ORGANIZED AND JUSTIFIED AS A FORMAL PROOF; it is problem solving.
· AD __________
· AE __________
· BC __________
·
CD __________
Prove that a point is on the perpendicular bisector of a segment if and only if it is equidistant from the endpoints of the segment. (For this, only use the First Five Axioms, i.e., through SAS congruence and not the isosceles triangle properties and theorems beyond.)