
Do all problems. Show any work that you do on the paper.
Construct with straightedge and compass a circle tangent to all 3 lines. WRITE down the main features of the construction (not every tick mark, but what the main points and lines and segments are).

This is the same problem as As 2.5. It is based on ideas in Lab 2 and As 2.6. References in B&B are on page 182-3. You are not told whethe the two lines that do not intersect on the page are parallel or whether they meet at a point 100 feet away, so the completely correct answer will not assume parallel (though a correct construction method for parallel will we close and was given substantial partial credit).
This solution has two parts. Both are important both should show up in the written description of important step
To talk about this, let's call the top of the two nearly parallel lines m and the other P. Let the line that intersects both be p. To construct the center, one needs a point equidistant from all 3 of the lines. But we can do this if we can make the point (a) be an equal distance from m and p and (b) be an equal distance from n and p. The set of points satisfying (a) consists of the two lines bisecting the 4 angles at the intersection of m and p (As 2.6 and also B&B Locus Thm 5, p 252, and GTC chapter 5. The two angle bisecting lines at the intersection of n and p is the set of all points satisfying (b). So construct an angle bisector of each an intersect them (there are two possible intersections that will lie on the page). That's the center.
What about (c) the set of points equidistant from m and n? If m and n are parallel, then this set is a line parallel to m and n that is in the middle between thm. If they intersect a long way away, one of the angle bisectors will look approximately parallel and half way in between, so if you construct that line, you can use it to intersect with one of the angle bisectors and get a close construction in practice. But you need to intersect two of three lines from (a), (b), (c). Other schemes for locating the center are probably not correct.
For the radius, simply drop a perpendicular from the center to any of the 3 lines.
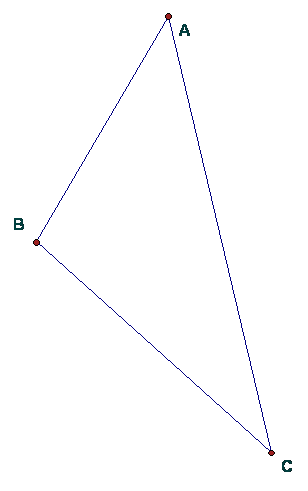
Given triangle ABC in the figure, construct the circle through points A, B, C.
What is the name given to this circle? __Circumcircle _
This was done in homework and Lab 1. Also see B&B 181.
On a line are points A, B, C and a ruler that makes points A and B correspond to numbers a and b. If B is the midpoint of AC, what number corresponds to C? (Answer should be an expression in a and b.)
Since B is the midpoint of AC, then b = (a+c)/2, so c = 2b - a.
Suppose that m and n are lines that intersect at O. If P is a point equidistant from the two lines, prove that P is on a bisector of one of the angles defined by the two lines.
(You can use any of the theorems that you know to prove this, except what you are proving, of course.)
This is the one direction of the if and only if proof
of As 2.6. Also see Lab 2. The first half of the proof of B&B, Locus Theorem
5, pp. 251-2 is a proof of this similar to what was expected here.
In this figure, E is on line AC and D is on line AB, and angles ABC, ACD, and ADE are right angles. Length |AB| = 4 and |AC| = 5.
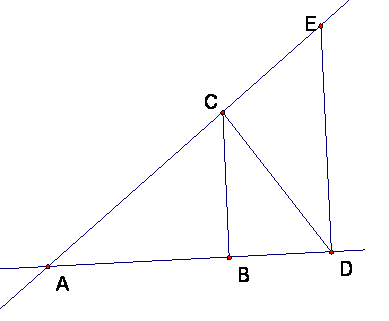
Compute an exact numerical value (i.e., not a decimal approximation) for the lengths of the following segments. Show your reasoning clearly enough to follow, but THIS DOES NOT HAVE TO BE ORGANIZED AND JUSTIFIED AS A FORMAL PROOF; it is problem solving.
The missing side BC of triangle ABC is provided by the Pythagorean theorem, BC =3. For the rest, by AA, triangle ABC is similar to triangle ACD and ACD is similar to triangle ADE and the scaling factor in each case is 5/4. So this gives.
· AD = (5/4)AC = 25/4
· AE = (5/4)AD = 125/16
· BC = 3
·
CD = (5/4)3 = 15/4
Prove that a point is on the perpendicular bisector of a segment if and only if it is equidistant from the endpoints of the segment. (For this, only use the First Five Axioms, i.e., through SAS congruence and not the isosceles triangle properties and theorems beyond.)
This is B&B Principle 10, page 88-89. Also see Notes on If and Only If.