Half a Dozen Ways to Understand the Product of a Halfturn and a Line Reflection

Understanding the composition of a half turn and line reflection is the key tool for simplifying and understanding more complicated compositions of rotations and line reflections or triple line reflections.  Here is the statement of what this composition is.  This will be followed by half a dozen proofs or outlines of proofs.  The reason for so many is that gives multiple ways to thinking about a basic transformation relationship.

Theorem:  Suppose that HA is a halfturn with center A and Rm is reflection in a line m not through A.  Let A' = Rm(A). 

Approach 1:  Basic Geometry (simplest but longest)

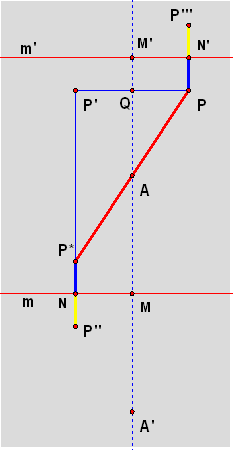
First, set up the figure with point A and line m.  Reflect A by Rm to get A'.  Also, apply the halfturn HA to m to get a parallel line m'.  The line AA' is the line through A perpendicular to m and m'.

Now take some point P and find its image from the definition of the half turn and the line reflection.

Compute P'' = Rm HA(P), first by finding P* = HA(P), and then P'' = Rm(P*).

By definition of halfturn, the red segments are equal: AP = AP*.  Connect P* with its reflection P'' by a segment; the segment intersects m at its midpoint N, so the segment P*P'' is divided into halves, the blue and the yellow segments..

Now apply HA to the segment P*P'' to get PP''' with midpoint N'. The segments P*P'', PP''' are both parallel to AA'.


Now compare with a glide reflection.

Observe that we can also get from P to P'' by first reflecting in line AA' to get P'. Let Q be the midpoint of PP', which is on line AA'.

This is the outline of what comes next.  Instead of transforming P to P'' by the halfturn and the line reflection in m, one can get the same result by reflecting P to P' and then translating parallel to AA' from P' to P''.  The key fact is that the distance P'P'' is constant and equal to the distance M'M , the distance between m' and m.  This distance is also AA'.  Since this distance does not depend on P, the glide reflection GAA' will send P to P'' for any choice of P, and this is what is to be proved.

The simple insight is that the distance from P' to P'' is the distance from P to line m plus the distance of P'' or P* to line m.  But the latter distance is the same as the distance from P to m', so the sum of the distances equals the distance between the lines. 

Now for the details: Vector P'P'' = P'N + NP''.  Since P'NMQ is a rectangle, vector P'N = QM.  Since N is the midpoint of P*P'', vector NP'' = P*N.

But this vector P*N = N'P, since P*NPN' is a parallelogram (diagonals bisect each other).  But N'P = M'Q because M'QPN' is a rectangle.

Thus vector P'P'' = P'N + NP'' = QM + M'Q = M'Q + QM = M'M.  This is what was to be proved.  Also, since AM = MA' = (1/2) M'M., the vector M'M = AA'.

This proves that the image P'' of P by RmHA is the same as the image of P by GAA'. 

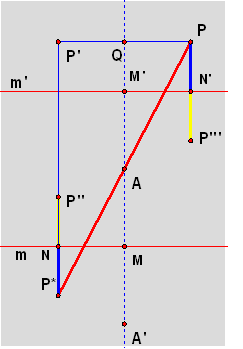
There is one loose end.  The figure that was drawn seems to depend on P being between m and m'.  Is the proof only valid for such P?

Here is a figure for P on the opposite side of m' from A.  The directions of some of the directed segments have been reversed.  For example, P'P'' = P'N + NP'' is still true, but NP'' is now negative relative to the direction of the other two segments.  Fortunately, the vector sums in the proof above, are still correct, so the proof is still correct.

The same direction-changing is true if P is on the opposite side of m from A.  This figure is left to the reader.  (We stress that is not really needed for the proof.)


Approach 2:  Fundamental Theorem 1 (image of a triangle)

We are told by a Fundamental Theorem that two isometries are the same if they agree on the 3 vertices of a triangle (any triangle).

If we pick a triangle to make our work easy, this gives a quick proof.

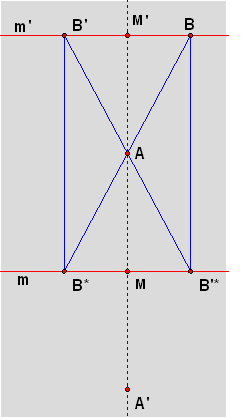
The points A and A', and the lines m and m' with their intersections M and M' with line AA' are the same as before.

Let B be a point on m' and B' its reflection in line AA'.  The points B* and B'* are the images of these points by HA.  It is easy to see that these points are on m.  The parallelogram BB'B*B*' is a rectangle because the sides B'B* and B'*B are parallel to the midpoint line M'M, which is perpendicular to m and m'.

We will now compare the image of triangle ABB' by the two isometries. 

Isometry RmHA does the following:

RmHA(A) = Rm(A) = A'.

RmHA(B) = Rm(B*) = B*.

RmHA(B') = Rm(B'*) = B'*.

Now compute the image of the same triangle by GAA'.  This by definition is the same as TR, where R = reflection in AA' and T is translation by vector AA'  Observe that vector AA' = vector M'M, etc.

Isometry TR does the following:

TR(A) = T(A) = A'.

TR(B) = T(B') = B*.

TR(B') = T(B) = B'*.

Thus the two isometries are the same: RmHA = GAA'. 


Approach 3:  Coordinate formulas (plug and chug)

It is possible to find formulas for both isometries and compare the two.  For simplicity, once A and m are given, coordinates can be chosen to make the formula as simple as possible.

Choose coordinates so that A = (0,0) and m is parallel to the y-axis with equation x = d.

Then line AA' is the x-axis.

Then the formulas (compare with problem 9.1)

Thus, for P = (x,y), Rm HA(x, y) = Rm(-x, -y ) = (2d+x, -y).

Now for the formulas for GAA' = TR, where R = reflection in AA' and T is translation by AA'.  The coordinates for A' can be computed from the formulas above as Rm(0,0) = (2d,0)

Then the formulas (compare with problem 9.1)

Thus, for P = (x, y), TR(x, y) = T(x, -y ) = (2d+x, -y).

So the formulas are the same and thus the isometries are the same for all points (x , y).

Approach 4:  Line reflection factorization of HA (the shortest)

If p and q are any two perpendicular lines at A, then HA = RqRp.

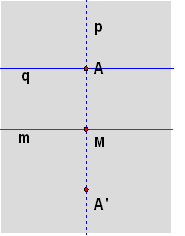
In the figure, A and m are given and A' is defined as Rm(A).  Then let q = line AA' and p = line through A perpendicular to q.

Then since HA = RqRp, the product Rm HA = Rm(RqRp) = (RmRq)Rp.

But the reflection Rp is the reflection called R in previous sections.  Also, (RmRq) is a translation that sends A to Rm(Rq(A)) = Rm(A) =  A'. This means that the translation vector is AA'.  This is the translation that was called T in the previous section.

Referring to the equation above, HA = (RmRq)Rp = TR = GAA'.  The proves the result.


Approach 5:  Another halfturn factorization (uses an inverse)

For this discussion, continue to use the figure from Approach 4.

From our study of halfturns, we know that HMHA  is translation by vector 2AB = vector AA'. Using the previous notation TAA' = T,  this says HMHA = T.

But also HM = RpRm, so the equation becomes RpRm HA = T.  Multiplying on the left by

Rp and using RpRp = identity, this equation yields RmHA = RpT. 

Using the notation R = Rp from before, this says RmHA = RT.  But this is is not the same equation as before, since in general TR is not the same as RT.  However since the translation T is parallel to p, the image of a point P reflected to P' and translated to P'' is the same as P translated to P* and then reflected.  The reason is that PP'P''P* is a rectangle.  In other words, in the definition of a glide reflection, one can reflect first, then translate, or translate first, then reflect.  The result is the same since the translation is parallel to the mirror. With this observation one concludes that RmHA = TR.

Approach 6:  Tracing a point (uses Fundamental Theorem 3)

The previous approaches have actually been proofs the relationship Rm HA = GAA'.  In none of these proofs did we use Fundamental Theorem 3 that says a triple line reflection (in lines not concurrent or all parallel) is a glide reflection.  The reason is that we used this RmHA = GAA' to prove that Theorem 3, so proofs must avoid circular reasoning.

However, now that the relationship RmHA = GAA' has been proved 5 times, it is time for a change of pace. In symmetry problems and construction problems, one can be given an isometry F that is known to be a glide reflection by Fundamental Theorem 3.  Then the question is to find the defining data, i.e., the invariant line and glide vector. 

One simple way to find this data is the midpoint method.  Pick two points P and Q and find the midpoints X and Y of PF(P) and QF(Q).  The invariant line is line XY and the glide vector is the vector P'F(P), where P' is the reflection of P in line XY.

If we set F = RmHA, will this work?  Look at the figure for Approach 1.  Clearly the midpoint of PP'' is on line AA' for any P.  The midpoint of AA' is M, so it is also on line AA'  This shows that line AA' is the invariant line of F.  The glide vector can be found by taking F of a point on this line.  The vector is AF(A) = AA'.

Another way to see that F is GAA' is to track A, computing F(A), F(F(A)), etc.  All these points lie on line AA', so line AA' must be the invariant line, because for any point P not on the invariant line, the track P, F(P), F(F(P), … is a zigzag.

A third way is to observe that points on a line s parallel to line AA' are all mapped to points on the line s', which is the reflection of s in line AA'.  This can only be the case when the line in the middle is the invariant line.