Math 487 Lab 9- part A

Math 487 Lab 9, Part A

What to turn in from Part A?

Lab 9 -- you can do it with Sketchpad or by drawing and construction on paper

For each experiment there is a figure that should be saved (Sketchpad) and turned in on paper. Turn in a printout or drawing on paper, whatever tool you use.

Also, answer a few questions.

The instructions for what to turn in are found in the blue boxes at the end of the experiments.

The first part of this lab is about Glide Reflections. You will need to read about the definition and the concepts of the glide vector and invariant line of a glide reflection. Some of this is in Brown, but the terminology is explained on this web page about Translations and Glide Reflections. The terminology for "orbits" can be found on the Orbit Page or the Transformations and Orbits Page

Also, this lab has variants for doing the lab with Sketchpad or on paper. See below for each version.

Link to Part B of Lab 9

Glide Reflections: How to glide reflect a shape with Sketchpad

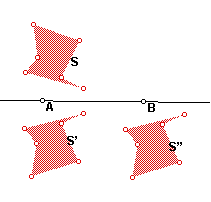
In a new sketch, draw a line AB.

Select the line and choose Mark Mirror from the Transform menu.
Select A, then B and choose Mark Vector AB from the Transform menu.
Draw a point P. Reflect P by the marked mirror line to get P' and translate P' by the marked vector to get P''. Then set G(P) to be P''.

This point P'' = TR(P), where R is reflection in the line AB and T is translation by AB. Thus G = TR, a composition. G can also be applied to a point in the same way:

Make a shape S.
Reflect S across the line to get S'.
Translate S by the vector to get S''.
Hide S’ if you only want to see S and G(S).

The transformation that takes S to S’’ is the glide reflection g_AB.

You can make a tool to perform this transform. Hide P' and select A, B, line AB and P and P''. Then Make New Tool. This tool will take two points as A and B and any object U and construct g_AB(U).

Glide Reflections: How to glide reflect a shape with straightedge and compass

Draw two points A and B and a line AB = m..

Draw a point P and construct the reflection P' of P in line m. (Drop a perpendicular to m through P and then mark off an equal distance on the opposite side of the line to get the reflection.)

Translate P' by AB to get P''. (Construct the line n through P' perpendicular to PP' and then mark off distance AB on n to get P'' so that AB = P'P''. If P is not on m, then ABP''P' is a parallelogram.)

Then P'' = G(P) for the glide reflection G = g_AB, which is by definition TR, where R is reflection in m and T is translation by AB.

To construct G of a shape, image points can be constructed one by one. However, recalling that for any shape U, G(U) is congruent to U, once the image of a couple of points is constructed the rest may be constructed from information from U. For example, to construct the image of a sqaure ABCD, once one has found the images G(A) and G(B), then the rest of the image square can be constructed from these points.

Exploration 1: Iterating G to be the orbit of a point

(You can use Sketchpad or graph paper or construct with straightedge and compass for this)

Draw a line AB and a point P not on line AB. Let G = g_AB be the glide reflection defined above.

Construct G(G(P)) = G²(P) and also G³(P) and G⁴(P).

Midpoints and the Invariant Line of G

Construct the midpoint of segment PP'' = segment PG(P) and also the midpoints of the segments G(P)G²(P), G²(P)G3(P), and G³(P)G⁴(P) .
You should find that these midpoints are collinear and equally spaced (by vector AB). See whether you can prove this. There is an explanation in Brown and on the Glide Reflection Information sheet..
Check that the points P, G(P) an G²(P) are collinear if and only if P is on the invariant line AB.

Parallels and vectors

Draw the line through P and G²(P) and also the line through G(P) and G³(P). Notice that each line is parallel to line AB. Can you see that all points Gⁿ(P) will be on one or the other of these lines.
Also, notice that G²= a translation T, so that T(G(P)) = G³(P), etc.

(If you construct the lines through P and P' parallel to AB, it may make this repetitive step easier.)

From Experiment 1: To turn in

The figure from this experiment.
Answers to these questions

Questions

For what other points C and D will the glide reflection by C and D be the same as the G defined by A and B?
Given an isometry, if you suspect it is a glide reflection, how can you find its invariant line and glide vector?

Goals of the section above and the following section:

Know and understand the standard definition of Glide Reflection.
Prove that if G is a glide reflection, there is a line m such that for any point P, the midpoint of P and G(P) is on line m. This line is called the invariant line of G. (Notice that this lets us find the invariant line even if we are not told what the points A and B are.)
Prove that the isometry G² is a translation, with translation vector 2AB (in the notation of the construction above.)
The orbit of a point P is an infinite set of points arranged in a "zig-zag" pattern, unless P is on the invariant line. (Explain what this means)

Detective Tools: Orbits and Tracks

Orbit of a Shape

Suppose G is a glide reflection. With Sketchpad, it is easy to start with a shape S and then construct images G(S), G²(S), G³(S), G⁴(S), etc. The set of these images is the forward G-orbit of S (for informatoin about this terminology, see the Orbit Page or the Transformations and Orbits Page for more details).

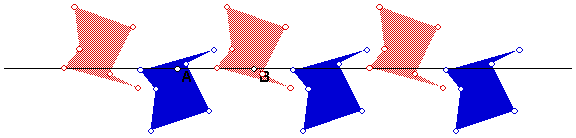
In this figure the shapes are colored differently, according to whether they = Gⁿ(S) for even or odd n.

What isometries will map an even shape to other even shapes? What isometries will map an odd shape to other odd shapes?

To make a figure like this by hand, it is probably worth while to cut out the shape from cardboard. Then construct a couple of key points of each image but trace the rest.

Track of a point

If P is a point, then one can also construct the orbit of point P, which is an infinite set of points. However it can be difficult to see the pattern in this disconnected set of points. It is easier to visualize if one makes a track of P.

Construct P' = G(P) and then construct segment PP'.
Then construct the sequece of segments (including endpoints) PP', G(PP'), G²(PP'), G³(PP'), G⁴(PP'), etc.

This constructs a sequence of points P, P', P'', P''', ... and connecting segments PP', P'P'', P''P''', ...

Such a track can be constructed for any transformation T, but if T = G a glide reflection, and if P is not on the invariant line of G, this track is a zigzag.

This track is relatively easy to construct on paper by hand.

Experiment 2: Generating a frieze pattern with squares

Make a pattern of squares like this.

With Sketchpad you can use a square-construction tool
By hand you can also construct squares, but it will be easier to take some graph paper and outline squares on the graph paper.

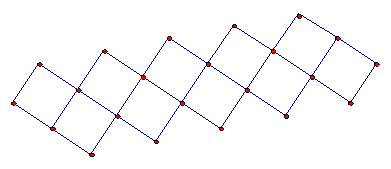
If you imagine this pattern being extended forever in both directions, what are the symmetries? In particular, what glide reflections are symmetries?

Construct a line as in the figure below, and let this be the invariant line of a glide reflection. Choose the glide vector for G so that the glide reflection of the first square (on the left on top) is the second square (the first one in the bottom row).

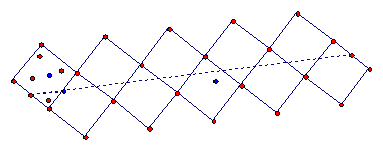
Make some asymmetrical design U in the first square and then construct G(U), which should be in the second square, and then G(G(U)), which will be in the third square (the second in the upper row). Notice that G(U) is not the reflection of the first square across their common side.

Continue constructing G of the images until you fill up all the squares.

This pattern is part of the G-orbit of U. It is also part of what is called an infnite frieze pattern. A frieze pattern is a pattern that among its symmetries a translation by a non-zero vectors, but all the translation symmetries of the figure should be parallel.

From Experiment 2: To turn in

The figure from this experiment.
Indicate on the figure the glide vector AB.

Experiment 3: A (possible) glide reflection by composing a line reflection and a 90-degree rotation

Construct this with graph paper or with Sketchpad. This time the instructions are for graph paper first.

Graph Paper Method

Draw the x-axis and the y-axis. Label the origin O = (0,0) and the line m, that is the line of points (x,y) with x = 1.

Make a simple asymmetrical design U contained in the unit square (the square with corners (0,0), (1,0), (1,1), (0,1)). Make the unit length about 1 inch so that the figure is not too small. It would be a good idea to make a one-inch square piece of cardboard and cut out a shape as a stencil.

Now let the transformation R be reflection in m. Let S be rotation by 90 degrees (counterclockwise) with center O. Let T be the composition RS (watch the order of the composition).

The goal of this experiment is to draw about 8 shapes that show the T-orbit of U. Then to answer the question.

Specifically, first rotate U by S and then reflect by R. Draw this new shape U' = T(U) on the paper. Then rotate U' by S and reflect it by R and draw this new shape U'' = T(U'). Continue until you have 8 shapes.

Sketchpad Method

In a new sketch, draw a point O and a line m. Let S = O₉₀ be rotation by 90 degrees with center O and let R = R_m be reflection in m. In this experiment we will study T = RS.
Pick a point Q and rotate Q by S to get Q' and then get Q'' = R(Q'). Hide Q'.
Select all and Make a New Tool that will construct T(Q) = Q''.

Now make a polygon interior U to use as a shape.

Apply the tool repeatedly to U and its images to get shapes of the T-orbit of U.

From Experiment 3: To turn in

State some good informal evidence that T is a glide reflection.
Save and turn in the figure from this experiment.
Choose a point P not on m and construct the track of P (see above).
Use the track of P to construct the invariant line and the glide vector AB of T.