Lattices and Tessellations

1. Lattices and Parallelogram Tessellations

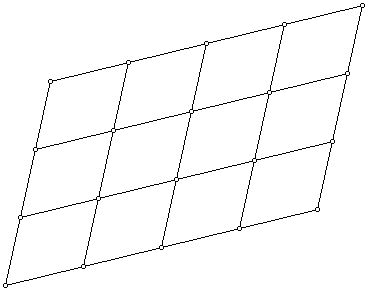
We say a shape tessellates the plane, if congruent copies of the shape can be laid down edge to edge as tiles cover a floor. We know some common shapes tile the plane. For example, equilateral triangles tile the plane; also squares or rectangles can be used. In fact general parallelograms tile the plane like this.

Experiment 1A: Sketchpad Construction of a Lattice

What is a lattice? A lattice is a infinite set of points in the plane obtained from a triangle A, B, C. The points are obtained by translating A by all possible vectors mAB + nAC, m and n being integers (including zero and negative integers. One can get the same lattice from different triangles.

1. In a new sketch, begin with a segment AB and mark vector AB. Then use this vector to translate B and its images and images of images to get a row of equally spaced points on line AB. For later use it will be helpful to construct about 5 such points. If he spacing is too wide for the screen, simply drag B closer to A. Also construct the same number of points by translating by vector BA. All the points are on line AB.
2. Next, draw a point C and mark vector AC. Translate all the points previously constructed on line AB by this vector and then translate the image and the image of the image to get a finite piece of the lattice defined by ABC.

Parallelogram Tessellations

1. MAKE A NEW PAGE in your document by Document Options>Add Page>Duplicate>1. Now you have a copy of your lattice page.
2. Construct construct 4 lines to form the parallelogram, 3 of whose vertices are ABC. Construct more parallel lines or segments to form a tessellation by parallelograms like the one in the figure. In principle, the construction could go on all directions forever to cover the whole plane.
3. MAKE ANOTHER NEW PAGE in your document by Document Options>Add Page>Duplicate>1.
4. This time pick 3 points P, Q, R on the lattice with these properties. (a) Triangle PQR is not similar to ABC. (b)Triangle PQR has no lattice points in its interior. (c) There are no lattice points on the sides, i.e., on segments PQ, QR, RP (except the end points).
5. Once you have triangle PQR, again construct lines that form a parallelogram so that P, Q, R and 3 of the vertices. Then construct a tessellation based on this parallelogram, as in the figure.
6. What should happen is this: (I) every lattice point is the vertex of one of the parallelograms of this new tessellation and (II) the area of triangle PQR = area of triangle ABC. (Can you shear the triangle P.

2. General Quadrilateral Tessellations

Experiment 2A: Hands-on Experiment with General Quadrilateral Tessellations

This shows that special quadrilaterals can tile the plane. But what if we take as a tile a "random" quadrilateral with no special shape?. Can we lay down tiles of this shape to cover the plane?

Try this out. Cut out a set of congruent quadrilaterals like this one, or one of your own choosing.

Assemble them like a puzzle to cover (tessellate) the plane. Do this! Then note carefully that adjoining shapes are can be moved one onto the other by an isometry. What isometry is this? (Save the figure by taping it to paper or tracing around the shapes onto paper.

Try another example. This time take a shape that is not convex and tile the plane with it. Answer the same question about how neighboring tiles are related by isometries.

Experiment 2B: Sketchpad Tessellation by General Quadrilaterals

In a new sketch, draw a quadrilateral ABCD (no special shape).

Create a tessellation with Sketchpad like the one you did by hand. An important feature of the Sketchpad construction is that if you drag any one of A, B, C or D to change the shape of the original quadrilateral, the shape of ALL the quadrilaterals will change so that all are congruent. And the tiles will still cover the plane. To do this you will need to use transformations. Save this figure!

Experiment 2C continued: The Midpoint Connection

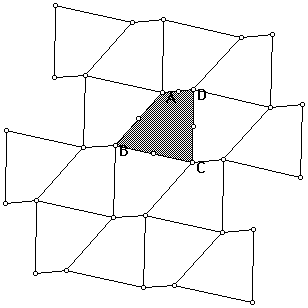
Form the midpoint parallelograms of the quadrilaterals and observe how they fit together. Do you see a lattice?

Construct the interor of ABCD and also construct the interiors of the other quadrilaterals that can be obtained from ABCD by translation (i.e., all "right side up").

What pattern so you see? Is there a lattice in the figure that come from the translations of these shaded quadrilaterals? How is this lattice related to the lattice of the midpoints?

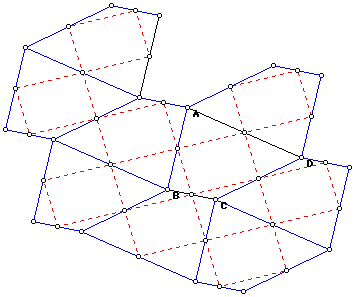
How is the area of a midpoint quadrilateral related to the area of ABCD? Can you see this in the figure?

3. Point Reflection and Translation

Let A be a given point in the plane, and let P be another point in the plane. We construct the point P’ the point reflection of P with center A, as follows: let P’ be the point on line AP distinct from P with |AP’| = |AP|. (Special case: if P=A, then define P’= A also.) In other words, A is the midpoint of PP'.

This defines a function or transformation H_A that takes P to P’. This transformation is also sometimes called point reflection or point symmetry. This transformation is the same as a half-turn, a rotation by 180 degrees.

In Sketchpad, point reflection in A is either rotation by 180 degrees with center A or dilation with ratio -1 with center A.

Recall several important properties of point reflections and then solve a problem using these properties. The properties are:

• Point reflections are isometries (i.e., point reflections preserve distance).
• A point reflection maps a line m to a parallel line m'.

Here is a curious geometry problem.

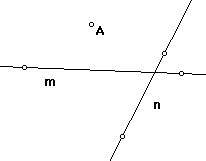
Version 1. Given two lines m and n and a point A, find a point M on m and a point N on n so that A is the midpoint of MN.

It may not be clear how to attack this problem, but point reflections give an approach to the problem. It can be reformulated thus:

Version 2. Given two lines m and n and a point A, find a point M on m and a point N on n so that N is the point reflection of M with center A.

Finally, there is a third version:

Version 3. Given two lines m and n and a point A, find a point M on m and on the image of n by the point reflection with center A.

• Create a sketch with point A and two lines, m = line BC and n = line DE.

• Construct the image n' of line n by the point reflection with center A.
• Define M to be the intersection point of m and n'; define N as the point reflection of M.
• Check that this really solves the problem. Think through why this solution works. What are the special cases that have no solution?
• How is this related to properties of a parallelogram?

One of the powerful concepts about transformations is the concept of composition. We can get some interesting geometric figures by composing point reflections.

1. In a new sketch, draw two points A and B and then draw a shape S as a polygon interior. Any irregular shape will do.



2. Now rotate S by 180 degrees with center A to get S'. Continue rotating by 180 degrees as follows: rotate S' with center B to get S''. S'' is obtained from S by the composition H_B H_A. From your observation what kind of transformation relates S and S''?
3. Continue adding to this figure with 180-degree rotations. Next rotate S'' with center A to get S'''; then rotate S''' with center B to get S'''.
4. Now start again with S and rotate with center B first, then A, for several steps.
5. Observe the pattern you get as you drag S or as you drag A or B. In particular, observe that some shapes appear to be translations of each other and some not. How are the shapes spaced? Is there any consistency as you drag S?

This experiment explains composition of point reflections in terms of elementary geometry.

This figure would usually be constructed from a triangle and its midpoints, but instead, construct the figure in a special way.

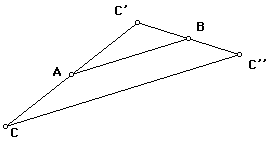
Start with segment AB and point C.

1. Rotate C by 180 degrees with center A to get C'. Then in the same way, take the point reflection of C' with center B. Connect the points as in the figure.
2. Measure the lengths of AB and CC''.
3. Explain why segment CC'' is parallel to segment AB, in the same direction and twice as long wherever you move C.
4. Add a shape S to the figure along with S', the point reflection of S with center A, and S'', the point reflection of S' with center B. Experiment by moving point C to various vertices of S. Notice how the corresponding points of the other shapes coincide with C' and C''.

If H_A is the point reflection with center A and H_B is the point reflection with center B, then C'' = H_B(C') = H_B(H_A(C)). If we ignore the intermediate step and move straight from C to C'', we can think of this as a single transformation. This transformation T is the composition of the two point reflections. We denote this as a product. This T = H_B H_A, and T(C) = C''.

Sketchpad can create a tool that will take A, B and C and construct C'' by the construction above.

One can also create a tool that will take A, B, and C and translation C by vector AB to get C' and translate C' by AB to get C''. Experiment to verify that C'' is the same from both constructions.

The Moral of this Story is that we can get exactly the same transformation T two different ways.

• T = H_B H_A
• T = T_AB T_AB , where T_AB denotes translation by vector AB.

One can learn a lot by finding relationships in figures, but some relationships that may be difficult to see in a static figure jump out when the figure moves. Such figures are possible with dynamic software for geometry such as The Geometer's Sketchpad.

• Draw a quadrilateral ABCD and construct the midpoints of the sides. Then connect these as in the figure to form a new quadrilateral EFGH of midpoints.

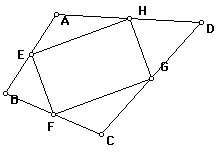
We have proved before that this midpoint figure is a parallelogram. Now let's construct ABCD from the midpoint figure.

If you see the connection between the quadrilateral figure and the triangle midpoint figure, it may not surprise you that there is a way to think about this figure using point reflections.

1. In a new sketch draw points A, B, C and P. Construct P' as the point reflection of P with center A.
2. Then construct P'' as the point reflection of P' with center B. Finally, form P''' as the point reflection of P'' with center C. The point P''' is the transform of P by a triple composition, P''' = H_C H_B H_A (P). What (single) transformation does this triple composition appear to be?



3. Investigate in the sketch. Connect P and P''' by a segment and construct its midpoint D. As you drag P around the plane, while leaving A, B, C fixed, does D move?
4. Explain these relationships using the figure. H_B H_A = H_C H_D. From this, H_D = H_C H_B H_A.

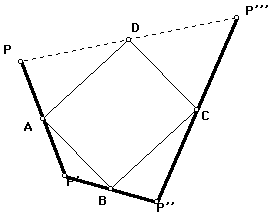
Related Problem: Construct a quadrilateral with vertex P given the midpoint parallelogram ABCD. Explain why there is a solution only if ABCD is a parallelogram and only one solution.

Experiment 4C: From parallelograms to general quadrilaterals

Return to your sketch with tessellation by parallelograms. Place a point P inside one of the parallelograms with vertices EFGH. Reflect P in each of the vertices E, F, G, and H and connect P to each reflection image point by a segment.

Now each of the images P' of P are also in a parallelogram. Reflect each of these points in the vertices of their parallelograms and each point to its images.

If you keep repeating this constructing and connecting points and their images, you will soon find you have formed a the same figure as in 2B and 2C, but this time starting with the parallelograms rather than with the general quadrilateral!

Question: If you imagine the quadrilateral tessellation pattern continuing on over the whole plane, what are the symmetries of this infinite figure?