
The class seemed to be figuring out good way to use geometrical language to play the Barycentric Battleship game. But since time was limited and each team tended to home in on one strategy, it seems a good idea to summarize some of the math in the game.

The strategy outline by Jason Gadek showed one important idea, which is the way each of the barycentric coordinates creates a family of parallel lines that can be used to describe the position of the point. For example, this shows the parallel lines for constant values of x, the coordinate that measures height over BC relative to A. You can draw in sets of lines for y and for z in the same way.
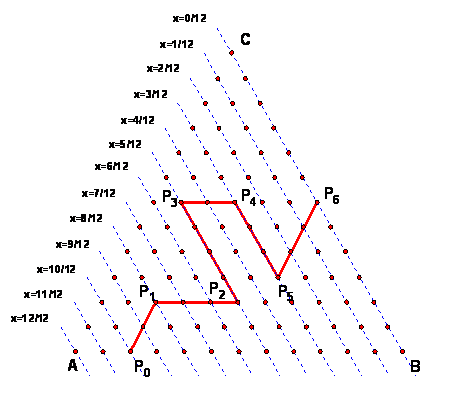
Using this approach, the point P0 is given by (x, y, z) = (10/12, 2/12, 0/12) = (1/12)(10,2,0).
Then the move to P1 moves on a segment of constant y two steps to the point P1=(1/12)(8,2,2). Next are 3 steps along constant z and increasing y to P3 = (1/12)(5,5,2).
A slightly different point of view focuses on specifying the move by giving names to each possible move. If a point is not on an edge, it has 6 possible moves. Each move is parallel to one of the edges of the triangle. Lets call move m1 the step parallel to side BC that moves in the direction of C and away from B (i.e, the move that increases z). Then the opposite move can be called –m1. Likewise, let m2 be the move parallel to CA in the direction of A (it increases x) and the move m3 the move parallel to AB in the B direction (it increases y). The moves in the opposite directions are –m2 and –m3.
The move from P0 to P1 can be described as -2m2 and the move from P1 to P2 as 3m3. The move from P2 to P3 is 4m1. This can be used to tell how to draw the next segment.
A transformation, or motion, of the plane called a translation is defined by an oriented segment. For example, the translation defined by points F, G, or translation by vector FG means that any point P is move to a point Q so that FGQP is a parallelogram (with a special case when F, G, P are collinear). In other words, FG and PQ are parallel, the same length and the same direction. Also, translation by a multiple of FG, such as (1/12)FG, means translation by FH, where H is the point on ray FG with |FH| = (1/12)|FG|. A negative multiple means that the point H was chosen on the opposite ray. It can be shown that (-1/12)AB = (+1/12)BA.
Using this concept, the move m1 becomes translation by (1/12)BC, m2 = translation by (1/12)CA, m3 = translation by 1/12)AB. Also, -2m2 = translation by (-2/12)CA and 4m1 = translation by (4/12)BC.
One important thing to note is that if we move by m1, then m2, then m3, we get back to where we started. In other words, this translation is the identity or the translation by the zero vector.
The key relationship between the "move" approach and the "parallel line coordinate" approach is what each move does to the coordinates (and their parallel lines).
For example, the move m1 increases z by 1/12 and decreases y by 1/12; x remains unchanged. Thus the sum of the coordinates is the same before and after the move; the coordinate sum stays the same after each move (as it should, since the coordinates always add up to 1).
This observation suggests a good way to represent the moves is by triples of numbers that tell that the move does to each coordinate. This means
For example, P1 is obtained from P0 by -2m2. With the number-triple notation, this means that we can add (-2/12(((1,0,-1) = (1/12)(-2,0,2) to (1/12)(10, 2, 0), the barycentric coordinates of P0 to get (1/12)(8, 2, 2), the barycentric coordinates of P1. Then the move from P1 to P2 is given by adding 3m3 = (3/12)(-1,1-0)=(1/12)(-3,3,0) to (1/12)(8, 2, 2) to get (1/12)(5, 5, 2).
This means that to find the result of -2m2 followed by 3m3, we simply need to add the number triples; add (-2/12(((1,0,-1) + (3/12)(-1,1-0)=(1/12)(-5,3,2) to the barycentric coordinates of the point.
This addition formula leads to a second big observation. If you only want to go from one point to another and don't care about the path, then you can take the steps in any order you want. For example, instead of moving -2m2 followed by 3m3, you can move by any of these translations:
You can trace these paths in the figure and see how they move the point P0 to P2 in each case. Notice that the move m1 is included in the last example. This figure shows these paths (some overlapping).
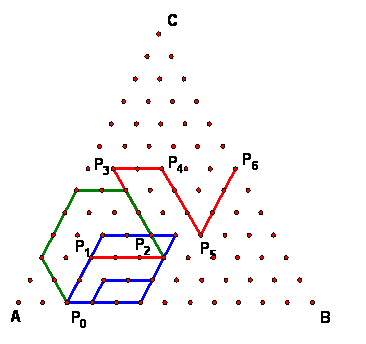
This commutative property for steps means that we can write the path as a sum (this is actually the sum of vectors) if we care only about the end result and not about the individual steps. Thus the paths above all give the same sum, bearing in mind that m1+m2+m3=0.