Answers to Assignment 9

Problem 9.1

The four reflections are

R₁(x, y) = (2a₁ - x, y)
R₂(x, y) = (2a₂ - x, y)
R₃(x, y) = (2a₃ - x, y)
R₄(x, y) = (2a₄ - x, y)

Part 1 - the answer is given

Part 2 - P'' = R₂R₁(x, y) = R₂(2a₁ - x, y)

= (2a₂ - (2a₁ - x), y) = (x + 2(a₂ - a₁), y) = (x, y) + (2(a₂ - a₁), 0)

This is a translation by vector (2(a₂ - a₁), 0), so the direction of the translation is perpendicular to the lines and twice the distance between then, in the direction from k₁ towards k₂.

Part 3 - P''' = R₃R₂R₁(P) = R₃(P'') = R₃(x + 2(a₂ - a₁), y) = (2a₃ - (x + 2(a₂ - a₁)), y)

= (2(a₃ - a₂ + a₁) - x, y)

This is line reflection in a line m parallel to the 3 lines, with equation x = c, where c = a₃ - a₂ + a₁

Part 4 - P'''' = R₄R₃R₂R₁(P) = R₄(P''') = (2a₄ - (2(a₃ - a₂ + a₁) - x), y)

= (x + 2(a₄ - a₃) + 2(a₂ - a₁), y) = (x, y) + (2(a₂ - a₁), 0) + (2(a₄ - a₃), 0)

This is a translation by vector + (2(a₂ - a₁), 0) + (2(a₄ - a₃), 0).
Since R₄R₃R₂R₁ was just computed as R₄(R₃R₂R₁), this is the product of two parallel line reflections in line m followed by line k₄. Thus the translation vector is 2(a₄ - c), where c is as above.

R₄R₃R₂R₁is the composition of the translation R₂R₁ by vector (2(a₂ - a₁), 0) and the translation R₄R₃ by vector (2(a₄ - a₃), 0), so R₄R₃R₂R₁is also a translation with translation vector equal to the sum of these two vectors.

Summary and Overview

To summarize, it should be clear that any composition of an odd number of lines parallel to the y-axis will have the formula (2e - x, y) for some constant e. So it is reflection in the line with equation x = e, where e is the alternating sum of the constants in the line equations: e = (a_n - a_n-1) + (a_n-2 - a_n-3) + … (a₃ - a₂) + a₁
The product of an even number of reflections will be have the equation (x + 2f, y) = (x, y) + (2f, 0), which is translation by vector (2f, 0). The constant f is also the alternating sum of the constants in the equations of the lines, but since the number of constants is even, this is the sum of differences (a_n - a_n-1) + (a_n-2 - a_n-3) + … (a₂ - a₁), representing the composition of n/2 translations.

Problem 9.2

Let m = line AB. See figure below.

Part I:

(a) T is a line reflection.

(b) The mirror line t of T is the line through A obtained by rotating line m by -45/2 degrees. So the angle from t to m = 45/2 degrees.

Reason: R can be written as R_mR_t, so T = MR = R_mR_mR_t,= R_t.

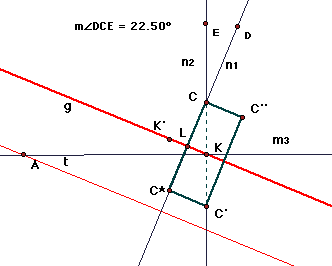
Part II:

(a) U is a glide reflection.

(b) If K is the foot of the perpendicular from C to m, the invariant line of U is the line g through K that is parallel to the line t of part I. The glide vector = K'K, where K is the reflection of K in line n1. See the figure for details.

There are several ways to figure this out. They will be discussed on a separate page.

Problem 9.3 (Composition of two rotations)

The centers called for in the question form a rhombus ADEC, with perpendicular diagonals intersecting at B. The angles of the rhombus at A and E are 60 degrees and the angles at D and C are 120 degrees. Thus triangle ADB is a right triangle with angles 30-60-90 degrees.
To see this, use the method of Brown 2.4. For example, the table below has rotated the figure to match up with the figure in Brown. RS = A60 B180 = C240
SR = B180 A60 = D240
S(RS) = B180 C240 = E 60 This looks a bit trickier. The line through C must make an angle of -60 degrees or +120 degrees with CB. Angle BCE does equal -60 degrees. If you prefer to work with + 120 degrees, then draw that ray but extend to a whole line and the line is the same as CE, so the intersection is the same.

Problem 9.4

There are a couple of ways to approach this. One is step by step. Start with 2 centers of rotation and form new centers as products as in the previous problem. Then use the new set of centers to keep building out new centers. All triangles are 45-90-45 triangles, so the geometry is simple.

A second method supplements the first by using symmetry to make it faster. If A is a 90 degree rotation center, then all the other centers you know can be rotated by 90 degrees to get new centers. (But be careful; this method alone will not pick up all new centers.

The third method is to realize that the pattern of centers is the p4 pattern we studied in lab. So use that. Match up what you know and fill in from knowing the p4 pattern.

Let AB = 1	Step by Step	p4 knowledge
90 - degree centers of rotation are K, M, O, A	Look for vertices X of isosceles right triangle ACX with right angle at C. Get X = O or K. Then look for vertices for OCY, get new Y = M and old one A. Also, for KCZ, get M. Note in all these triangles the distance between 90-degree centers = 2 (exactly). There are no points at distance 2 from A besides K, M, O.	We know that C is the center of a square with vertices being 90-degree centers. Since A is one vertex, K, M, O are the others. Same reasoning \|AK\| = 2 means no more such centers.
180 - degree centers of rotation are E, I, C	Look for vertices X of isosceles right triangles RSX with 90-degree centers forming the hypotenuse RS. The only new ones are AOE, AKI.	Since the 90-degree centers form a tessellation by squares with 180-degree centers at the centers of the squares, look at squares with sides AB and AO to get E, I and C.
Only translates of A are M and A.	Translations are given by composing halfturns. Don't forget there is a halfturn centered at the 90-degree centers (since 90 + 90 = 180). Starting at A, look at all the other centers and translate. A180 C180 (A) = M A180 E180 (A), etc. are all "off-screen."	The translation vectors in p4 are all vectors between centers of the squares, the 180 centers. These translate square vertices (90-degree centers) to opposite vertices and not adjacent vertices. A by one of the products.
None	There are no glide reflections that are products of these rotations.	Ditto.

Problem 9.5

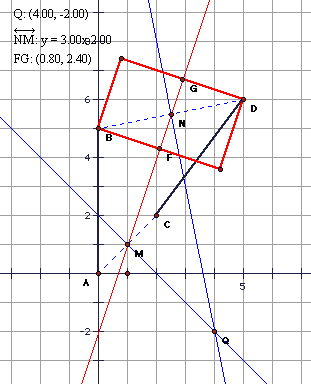
Segments AB and CD plotted on graph paper.

Constructions:

Center Q of rotation = intersection of perpendicular bisectors of AC and BD.
Invariant line of glide reflection is line MN, through midpoints of AC and BD.
Vector FG constructed from feet of perpendiculars to MN through B and D, since D = image of B. So glide reflection = G_FG.