Answers to Problems 3.3 and 3.4 from 3A

Problems 3.1 and 3.2 were explained in class.

3.3 Dilations and midpoints

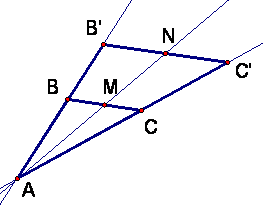
Let ABC be a triangle and let B' be a point on AB and C' a point on AC with |AB'|/|AB| = |AC'|/|AC|.

• If M is the midpoint of BC and N is the intersection of line AM with line B'C', prove that N is the midpoint of B'C'.

Proof

The strategy is to see that triangle ABC is similar to triangle AB'C' with scaling ratio K and that triangle ABM is similar to triangle AB'N with the same ratio K because of the common sides AB and AB'.

For the first pair of triangles:

Triangle ABC is similar to triangle AB'C' by SAS because of the shared angle and because we are given |AB'|/|AB| = |AC'|/|AC|.   Call this ratio K.

• By corresponding parts, |B'C'|/|BC| = K, so |B'C'| = K|BC|.
• In addition, angle ABC = angle AB'C'.  But this implies angle ABM = angle AB'N since these are the same angles.

For the second pair of triangles:

Triangle ABM is similar to AB'N by AA because of the shared angle BAM = angle B'AN and angle ABM = angle AB'N.  Thus by corresponding parts, |B'N|/|BM| = |AB'|/|AB| = K, so |B'N| =K|BM|.

Combining with the ratio that defines the midpoint:

Since M is the midpoint of BC, |BC|/|BM| = 2.  Since N is on segment B'C', it will be the midpoint of B'C' if B'C'|/|B'N| = 2.

If we write this ratio using the scaling from the similar triangles, we get |B'C'|/|B'N| = (K|BC|)/(K||BM|) = |BC|/|BM| = 2.

Thus, N is the midpoint of B'C'. QED

3.4 Nested isosceles

Let ABC be an isosceles triangle with AB = AC. Let D be a point on AB with CD = CB. If |AB| = 63 and |BC| = 17, what is |BD|? Show your reasoning.

Solution:

Since the triangles ABC and CDB are isosceles, with a shared angle

• Angle BCA = angle CBA (isosceles)
• Angle CBA = angle DBC (shared)
• Angle DBC = angle BDC (isosceles)

Thus triangle ABC is similar to triangle CBD by AA.

By corresponding parts, |BD|/|BC| = |BC|/|BA|, so |BD| = 17*17/63, which is approximately 4.59 (but the exact answer is what we want here).