Math 444 Quiz 4
NAME _______________________________________________
Problem 1 (Short Answer)
Suppose that each of E, F, G, H, J and K are glide reflections. Let U = EFGHJK.
With this information it is not possible to say precisely what kind of isometry U is, but one can narrow down the possibilities. Circle each name of a kind of isometry below when U could be an isometry of that type (for some choice of glide reflections). Then in a sentence, give a reason for your answer.
(a) Identity (b) Line Reflection (c) Point Reflection
(d) Translation (e) Rotation (f) Glide Reflection
Reason:
ANSWER: Circle a, c, d, e. Reason is that U is the product of 18 line reflections. Since 18 is an even number, one can also write U as the product of 2 line reflections. The circled items are the isometries that can be written as a product of two reflections. This is brought together in Brown, Thm 26, which uses Brown, Thms 15, 22, 23.
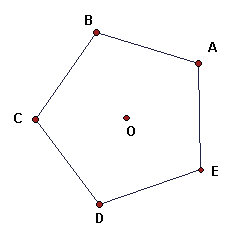
Problem 2 (Short Answer) This figure is a regular pentagon.

(a) How many rotation symmetries does this figure have? __________
(b) How many line reflection symmetries does this figure have? ___________
(c) Let line m = line OE, For what line n is RmRn = O144? _____________
(d) What symmetry is ROBROEROC? __________________________ (Give precise name or description)
Answer: (a) 5 (b) 5 (c) OD (d) Line reflection in OE. Notice that (c) and (d) are really the same kind of problem. Since O144 = ROBROA, (c) can be rewritten as Rn = ROEO144 = ROEROBROA.Problem 3 (Answer and Construction)
Given the points A, B, C in the figure,
(a) Tell what transformation T = A180 B180 C180 is.
Answer: T = __________________________________________
(b) Construct (with straightedge and compass) the defining data for this transformation.

Answer: Answer is D180.
Construct D so that ABCD is a parallelogram. This is covered extensively in
Lab 9 and Brown Section 2.3.
Problem 4 (Answer and Construction)
Given A and B in the figure,
(a) Tell what transformation A120 B90 is. Answer: ______________
(b) Construct (with straightedge and compass) the defining data for this transformation.

Answer: C210. The rotation angle of 210 degrees is the sum 120 + 90. Is it twice the exterior angle of angle ACB. The angles add when rotations are composed. See details in Brown 2.4, paying attention to which line reflection is first and which is second.
The construction of C is just as in Brown, figure 2.25; triangle ABC has interior
vertex angles 60, 45, 75. In this quiz problem C is above the line AB on the
page. The position of the lines is very sensitive to the direction of the rotation
and the careful choice of which line is first to get the correct one of the
two rays that, for example make an angle of 60 degrees with AB at A. To get
this right, one must study the method and reasoning with some care.
Problem 5 (Definition and short proof)
(a) State the definition of an isometry. (Note: A definition is a complete sentence with just the definition -- no extra stuff that you know.)
Answer: Brown page 12.
(b) It is said that isometries of the plane preserve angles. What does this statement mean, precisely?
Answer: If T is an isometry, for any angle ABC, the angle ABC is congruent to angle A'B'C', where A' = T(A), B' = T(B), C' = T(C). (A less wordy answer is ok, but it should have the points A, B, C in the explanation or probably the sentence will be rephrasing the question.)
(c) Prove your statement in (b), using the definition in (a).
Answer: Brown, Theorem
3. Proof uses SSS.
Problem 6 (Construction)
The two segments AB and CD are congruent.
Construct the defining data (invariant line m and glide vector EF) for a glide reflection G so that G(A) = C and G(B) = D.
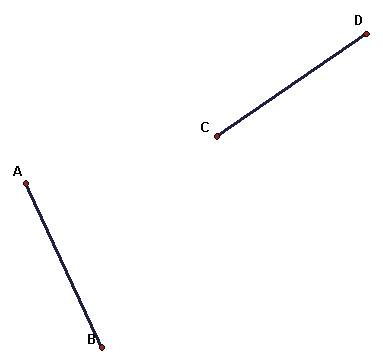
Answer: Let M be the midpoint of AC and let N be the midpoint of BD. Then line MN is the invariant line of the glide reflection. To find the vector, define A' as the foot of the perpendicular line from A to line MN and construct C' as the foot of the perpendicular from C to line AB. The vector A'C' is the glide vector. (Note: There is only one possible invariant line, but there are many pairs of points XY that define the same vector and the same translation as A'C'. For example, if one constructs B' and D' as feet of perpendiculars to line MN in the same way, then the vector B'D' is also a correct answer.)
To see how this works, for any point U, reflect U across line MN and the translate by A'B'. If A'' is the reflection of A across line MN, then the triangle AA''C is a right triangle with one leg perpendicular to line MN and one parallel to it. The same is true if you reflect B to B'' and construct triangle BB''D.
See more information at link to Glide Reflection Facts.
Problem 7 (Short Answer)
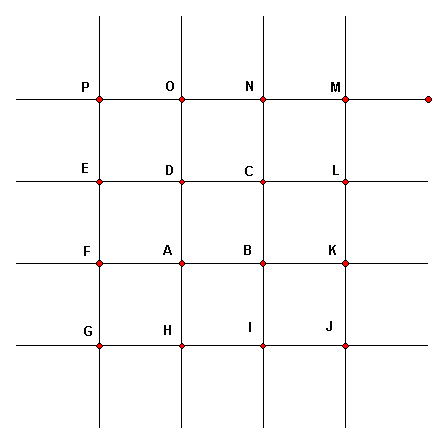
The figure below is part of an infinite pattern of squares. Let S = A90 and T = C90. These questions are about the collection of all isometries that can be formed as products (compositions) from S and T (such as SSTTTSTTSTTT, etc.)
(a) Which of the labeled points are centers of 90-degree rotations that are products formed from S and T? __________________________
Answer: OMECAKGI
(b) Which of the labeled points (not already included in (a)) are centers of 180-degree rotations that are products formed from S and T? __________________________
Answer: The other labeled points -- PNDLFBHJ
(c) Are there any unlabeled points inside square GJMP that are centers of 180-degree rotations that are products formed from S and T? Yes or No? _____________
Answer: No
(d) Which labeled points are images of point A by translations that are products formed from S and T? __________________________
Answer: OMK
(e) Which labeled points are images of point A by glide reflections that are products formed from S and T? __________________________
Answer: There are no glide reflections that are products of S and T, so there are no such points.