NAME __________________________

Do all problems.

Problem 1

Let ABCDP be a pyramid with square base ABCD and 4 faces that are equilateral triangles.

a)      Compute dihedral angle between a triangular face and the square base.

Answer (show work below) ____________________

b)      If the length of the side of the square base is s, compute the altitude and volume of the pyramid.

Answer (show work below) ____________________

Problem 2

Let ABC be a triangle with AB = AC = x.  Also let D be a point on AB with CB = CD = y.  Find the distance BD.

Problem 3 (Short Answer) This figure is a regular pentagon.

(a)    Let line m = line OE, For what line n is R_mR_n = O₇₂? _____________

(b)   What symmetry is R_OBR_OER_OB? __________________________ (Give precise name or description)

Problem 4 (Symmetry Short Answer)

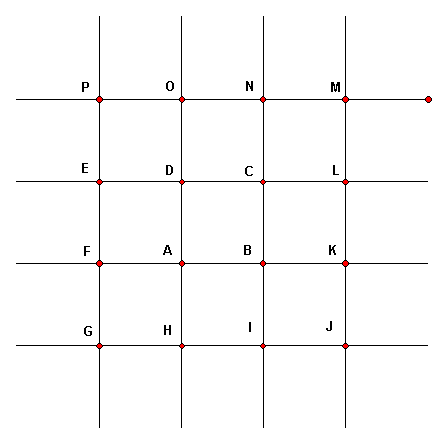
The figure below is part of an infinite pattern of squares.  Let S = A90 and T = C180.  These questions are about the collection of all isometries that can be formed as products (compositions) from S and T (such as SSTTTSTTSTTT, etc.)

(a)    Which of the labeled points are centers of 90-degree rotations that are products formed from S and T? __________________________

(b)   Which of the labeled points (not already included in (a)) are centers of 180-degree rotations that are products formed from S and T? __________________________

(c)    Which labeled points are images of point A by translations that are products formed from S and T? __________________________

(d)   Which labeled points are images of point A by glide reflections that are products formed from S and T? __________________________

 Problem 5 (Composition Answer and Construction)

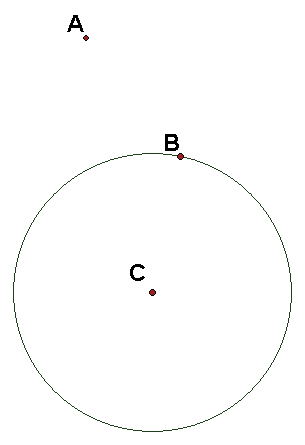
Given A and B in the figure,

(a)    Tell what transformation A₁₂₀ B₂₄₀ is.  Answer: ______________

(b)   Construct (with straightedge and compass) the defining data for this transformation.

Problem 6 (Construction)

Given the point A and the point B on the circle, construct a circle through A that is tangent to the circle at B.

Problem 7

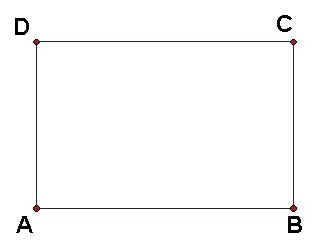
Given the rectangle below, construct a square with the same area.

Problem 8

Prove one of these two statements.

a)      Let a1 and a2 be parallel lines at distance d from each other; also let b1 and b2 be parallel lines at the same distance d from each other.  Assuming a1 is not parallel to b1, prove that the points of intersection of these lines form a rhombus.

b)      Given any quadrilateral ABCD, let M and N be the midpoints of AB and CD and let P and Q be the midpoints of diagonals AC and BD.  Prove that these 4 midpoints form a parallelogram.  Note: There are some special cases where the 4 midpoints are collinear.

Problem 9

Do either part (a) or (b) but not both.

a)      Prove that the perpendicular bisectors of the sides of a triangle are concurrent.

b)      State and prove the Pythagorean Theorem.