Dilations and Thales Figures

The Thales figure is a truly basic one in geometry.  There are many relations within it and many ways to think about it. One approach to organizing these ideas is to think of a scaling transformation of the plane called a dilation.

 

Let O be a point in the plane and let r > 0 be a positive real number.  Then for any point A in the plane, we define A', the dilation of A, with center O and scaling ratio r, to be the point A' on ray OA so that OA'/OA = r.  We also think of this as OA' = rOA, so that the length OA is scaled up or down by ratio r.

 

The new point of view is that we think of the dilation with center O and scaling ratio r as a rule, or function, or transformation, that takes every point A to a new point A'.  We can take any set S of points, a triangle, a circle, a line and dilate the points in S to get a new set S'. What's more the new figure S' is similar to the old figure.  This means that any dilation is a rule for expanding or shrinking all figures in the plane, much as a copy machine can scale letters and pictures on a page.

 

We can also define dilations for negative ratios r < 0.  In this case, when we write OA'/OA = r, we interpret this to mean that |OA'|/|OA| = |r|, but the direction of OA' is opposite that of OA, so A' is on the opposite ray of OA.

The Basic Geometry is Thales Figure

Here is a figure showing dilation by positive r.  By SAS, the triangle A'OB' is similar to AOB, so corresponding angles are equal, lines A'B' and AB are parallel and |A'B'| = |r||AB|.

 

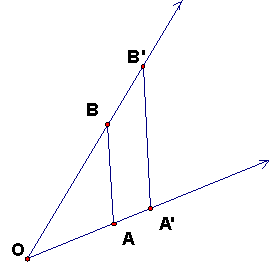
Here is a figure showing dilation by negative r.  By vertical angles, SAS still gives the same similar triangles and the same consequences, including |A'B'| = |r| |AB|.

 

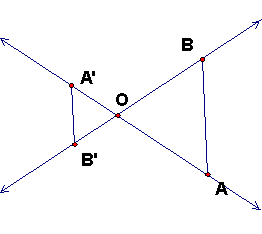
This last equation is key: |A'B'| = |r| |AB| is the fundamental scaling property of dilations. It means that any distance |AB| is scaled by |r|, not just the radial distances from O.

 

Key Theorem:  If C is a point on segment AB, then C' is a point on segment A'B', with A'C'/A'B' = AC/AB.  As a consequence the dilation of the line AB is a line; it is the line A'B' which is parallel to AB.

 

Proof:  C is on segment AB if and only if |AC| + |CB| = |AB|.  Now if this is true, then |A'C'| + |C'B'| = |r| |AC| +|r| |CB| = r |AB| = |A'B'|, so C' is on segment A'B'.  This implies that if 3 points are on a line, their dilations are also on a line, so any point C on line AB is dilated to a point on line AB.  From Thales we see the lines are parallel.

Understanding Geometrical Figures from a Dilation Approach

Trapezoids and Diagonals

This figure, with parallel AB and CD, can be analyzed from a dilation approach.  Think of O as the center and C = A' and D = B'.  Then r = OC/OA = OD/OB = CD/AB.

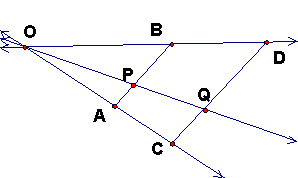
Then for ratios along OA, we have OC = r OA, so AC = OC – OA = (r - 1) OA.  In the same way, OB = (r - 1) OB.

 

If P is any point of AB and Q is intersection of line OP with line CD, then since dilation scales all distance by r, the ratio CQ/CD =( rAP)/(rAB) = AP/AB.  This means that the ratio that tells the location of P on line AB is the same as that of Q on CD.  In particular, if P is the midpoint, then this ratio = ½, so Q is the midpoint of CD if and only if P is the midpoint of AB.

 

Finally, if we draw lines BC and AD, and call the intersection I, then I is the center of a dilation that dilates A to D and B to C.  Thus the line PI intersects CD in a point U, for which AP/AB = DU/DC.  This is not the same as Q except when the ratio is ½.  This means that the point I is also on the line through the midpoints.

Constructing Dilations the Old-Fashioned Way - with Parallels 

What if we have a triangle ABC and a point O on a sheet of paper.  Let A' be a point on line OA.  Then if we want to dilate the whole triangle by the ratio r = OA'/OA, we can do it with parallels.

 

 

Then A', B', C' are dilations of A, B, C with the same ratio r = OA'/OA (a signed ratio).

The line B'C' should be parallel to line BC, and the triangle A'B'C' is similar to ABC by SSS, since each side length is multiplied by |r|.

 

This construction works on paper.  It is a bit laborious to construct parallels with straightedge and compass, so traditional draftspeople used special parallel rules.  This construction also works with Sketchpad.  If you use Sketchpad, you can drag the points A, B, C to change the shape of the triangle.  Also, drag A' along line OA to change the ratio r.  Especially check the appearance as the ratio changes from positive to negative.

 

Constructing Dilations a Faster Way – as a GSP Transform

Fixed Ratios in GSP

Since dilations are transformations of the plane, they can be found in the GSP transform menu. Let's try an example.  Draw some objects with with Sketchpad, say a segment, a circle, a triangle.  Then draw a point O as well.

Now see how a new copy of the figure has been created.  You can check that, as theory predicts, all lengths, including circle radii and circumferences, have been scaled by the ratio you chose.  Also see that if you draw lines from O to any of the original points, the line passes through the dilation image of the point.

 

Now repeat this experiment with a negative ratio.  If you don't want to create a new sketch, you can just Undo your way repeatedly back until you only have the original figure.  Again, examine the results for the key facts: scaling and the points A' are on the lines OA.

An Experiment with Ratio + or – One-half

 

Draw a triangle ABC and a point O.  Dilate the triangle ABC with center O and ratio ½.

 

Hide the dilated triangle A'B'C'.  Now dilate ABC by ratio –1/2.  Construct the segments AA', BB', CC'. 

 

Dynamic Ratios in GSP

This is rather nice, but the real power of Sketchpad dilations comes from a dynamic choice of ratio from the figure itself.  This is done by Marking the Ratio.  This can be done several ways.  Here is the most common:

 

Common Tangents of Circles

 

Starting with segments:  Construct two parallel segments AB and CD so that the end points can be dragged to different positions.  Specifically,

Next we will set up the dilation with center O that will dilate AB to CD. 

 

Reversing the Process – Starting with Circles