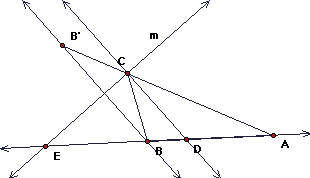
Begin with points A and B and a line m. We have seen how to construct a billiard path or the path of a beam of light that is reflected from A to B. We do this by reflecting B in m to get B'. Then segment AB' intersects m in point C.

Now construct the lines through B and C perpendicular to m. The line through B passes through B'. Let the intersection of the line through C with line AB be called D. The two lines BB' and CD are parallel.

We can apply Thales' Theorem to the triangles AB'B and the line CD to get the equality DA/DB = CA/CB'. But CB' = CB, so DA/DB = CA/CB'
For any triangle ABC, construct the ray that is the bisector of angle C.
|
Let D be the point of intersection of the angle bisector with segment AB. Then construct line CD and construct line m as the line through C perpendicular to CD. This is part of the figure on the previous page. Complete the figure and prove the following theorem: |
|
Interior Angle Bisector Ratio Theorem. For any triangle ABC, the (interior) bisector of angle C intersects segment AB in a point D so that DA/BD = CA/CB.
Line m in this figure is the exterior angle bisector of angle ACB. (Why?) Let E be the intersection of m with line AB. Add a line to the figure to prove this theorem:
Exterior Angle Bisector Ratio Theorem. For any triangle ABC, the exterior bisector line m of angle C intersects line AB in a point E so that EA/EB = CA/CB. Special Case: Exterior bisector m is parallel to line AB if and only if the triangle is isosceles, with CA = CB.