Read Berele-Goldman, Sections 8.1, 8.3, 9.1, 9.2
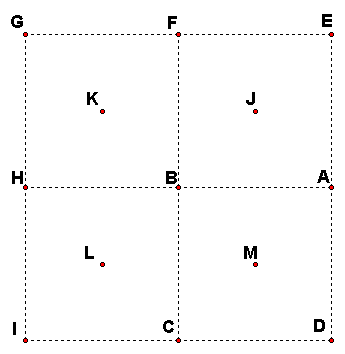
10-1: This figure is made of squares, with the centers of the squares labeled J, K, L, M.

Note: There was an error on the original sheet. There are two corrections in red. One is the correct answer for F90 and one is the correct item F270 in the first column for the given answers.
The goal of this exercise is to begin with S = A90 and T = B90 and to write rotations with centers at the other points as products of S and T. For a number of cases you are asked to do this explicitly. In this table,
a) Fill in column 2 by writing the given rotation as a product of two rotations already known from above as products of S's and T's.
IMPORTANT: There is more than one correct answer in each case. The best check of your answer for a case like C90 is to apply your transformation from columns 2 and 3 to C and see that C is transformed to itself. Then check that the angles add up correctly.
b) Fill in column 3 by writing the given rotation as a product of S's and T's.
c) Explain below the table what are all the centers of rotations that are products of S's and T's and how you would prove this.
If you have an isosceles right triangle XYZ (labeled counterclockwise around the triangle), with right angle at Z, then X90 Y90 = Z180. If the rotations are known at Z and Y, then solve for X90 by X90 = X90 Y90 Y(-90) = Z180 Y(-90) = Z180 Y270.
For example, F90 B90 = J180 in the figure above, so F90 = J180 B270= TSTTT.
d) Also, tell what are the translations that are products of S's and T's. In particular, is the translation that takes A to B such a product? If so, what is the product?
The translation U that takes A to C and the translation V that takes A to F and their inverses and all their compositions. For example, the translation W that takes A to H is the composition W = UV. (You could choose U and W or V and W and other possibilities as a basic pair of translations instead.)
IMPORTANT: You cannot get from A to B by a translation that is a product of S's and T's. This is easy to see if you add a symmetric pattern such as the one in Lab 8 Case 2 that has these rotations as their symmetries. Then the pattern around A is not a translation of the pattern around B.
|
Transformation |
Product of 2 known rotations |
Product of S's and T's |
|
J180 |
B90 A90 |
TS |
|
F270 |
B90 J180 |
TTS |
| F90 | J180 B270 or B90 A90 B-90 | TSTTT |
|
F180 |
F90 F90 |
TTSTTS |
|
M180 |
A90 B90 | ST |
|
C90 |
A270 B180 or B(-90) A90 B90 or | SSSTT or TTTST |
|
E90 |
A180 B270 | SSTTT |
|
K180 |
B90 F90 or B90 J180 B270 | TTSTTT or TTSTTT |
|
H90 |
K180 B(-90) | TTSTT |
|
Translation that takes B to E |
J180 B180 | TSTT |
|
Translation that takes A to F |
A180 J180 | SSTS |
10-2: Draw a point A and a line m. Let M be reflection in m.
a) Explain clearly how you know that for any rotation S with center A, the product MS is a glide reflection.
Let B be the point on m so that p = line AB is perpendicular to m. Construct n through A at an angle = one-half the rotation angle so that Rp Rn = S. Then MS = (MRp) Rn = B180 Rn = glide reflection. The invariant line is the line through B perpendicular to n. The glide vector is the vector B'B, where B' is the reflection of B in n.
b) Then draw A and m and construct the invariant lines of the glide reflections MA90, MA180, MA270.
Construct B as above. The lines n through A make angles of 45 degrees and 90 degrees with line AB. Then the glide reflection's invariant lines through B make angles of 45 degrees and 90 degrees with m.
c) Indicate the glide vector (the translation vector used in defining the glide reflection) of each of these isometries.
Construct B' as above.
Turn in Problem 9-4 along with Assignment 10A for full credit.