Assignment Due Friday 11/2

This assignment is closely linked to the Math 487 lab of Wed., 10/31/01

1. Prove that if a point A is on a circle c with center C, then a line m through A is tangent to c if and only if m is perpendicular to the radius CA.

2. Given two lines m and n intersecting at point O.  Let P be any point; denote the foot of the perpendicular to m through P by M and denote the perpendicular to n through P by N.  Prove that |PM| = |PN| if and only if P is on the angle bisector of angle MON.

3. Use 2 to prove that a point P is the center of a circle tangent to two intersecting lines m and n if and only if P is on the angle bisector of one of the 4 angles defined by the two lines.  Explain why this is the same as the locus statement in Part B of the lab.

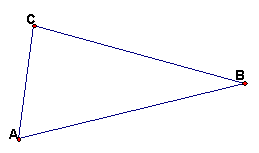
4. In a triangle ABC, prove that the angle bisectors of angles, A, B, and C are concurrent at a point I.  Also prove there is a circle centered at I that is tangent to all 3 sides.  Construct this circle in the example below (or draw your own triangle for the construction; just don’t choose an isosceles triangle) with straightedge and compass.

5. Suppose m1 and m2 are parallel lines distance d apart.  Also suppose n1 and n2 are parallel lines the same distance d apart (but not parallel to m1 and m2).  Then the 4 lines are the 4 sides of a parallelogram.  Prove that this parallelogram is a rhombus. (Note:  This is a figure like that formed by the dashed lines on the first page of Inv. 3 of Exp. 5.3.  You can easily draw such a figure using the two sides of a ruler to draw 2 parallel lines whose distance apart is the width of the ruler.)