This theorem is the centerpiece of this assignment.
Carpenter Locus Theorem. Given 3 points A, B, C, angle ABC is a right angle if and only if B is on the circle with diameter AC.
This is an if-and-only-if statement. Here is detail about one direction. The look below for the assigned problem based on these figures.
Discussion of what is to be proved:Let M be the midpoint of AC. Construct segment BB’. Based on observations from earlier explorations, what do you conjecture is the relationship among the lengths of segments MA, MB, and MC? You can construct do some measurements or construct the circle with center M through B and get some evidence for this conjecture, but the goal here is an explanation. The following figures will give some approaches for a proof.
In each case prove some relationships in this figure sufficient to prove the conjecture above. (You can use what you already proved in homework.) Notice that the points that are constructed initially in the figure differ each time, and that a point that appears to be a midpoint, for example, must be proved to be a midpoint if it is not constructed as a midpoint.
Figure 1. Construct the right triangle ABC as above (use the script). Let M, N, O be the midpoints of CA, AB, BC. Construct segments MN and MO and MB.
Figure 2. Construct the right triangle ABC as above (use the script). Let M be the midpoint of CA. Construct the lines through M perpendicular to segments BA and BC. Let A’ be the foot of the perpendicular to BA and let C be the foot of the perpendicular to BC.
Figure 3. Construct the right triangle ABC as above (use the script). Let P be the midpoint of BA. Construct the perpendicular bisector of side BA. Let the perpendicular bisector intersect AC at point Q.
Problem 1. Prove one direction of the Carpenter Locus Theorem 3 ways.
Given a right triangle ABC with right angle at B. If M is the midpoint of AC, prove that MA = MB = MC in 3 separate proofs.
Each of the proofs 1, 2, 3 should begin with the steps described in the recipes for Figures 1, 2,3 above. While the proofs should be self-contained, you should definitely quote what you have proved about isosceles triangles, kites, and perpendicular bisectors as needed to make the proofs clear and concise.
Problem 2. Prove the other direction in the Carpenter Locus Theorem.
Read Exploration 4.3 and use the ideas there to prove that if AC is a diameter of circle p, and if B is on p, then angle ABC is a right angle.
Problem 3. Consider the construction in 4.2, Investigation 2. The figure on page 46 appears to be a triangle with O the midpoint of segment BC. How do we know this? Prove that angle BOC is a straight angle and also prove that OB = OC. (Note: B and C are constructed from A by line reflection, so you can assume that line k is the perpendicular bisector of AB and line j is the perpendicular bisector of line AC. How is this related to Problem 2?
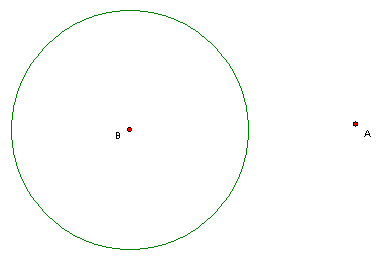
Problem 4. For the point and circle below, construct with straightedge and compass the two tangent lines to the circle that pass through A. Be sure to leave the construction marks showing. (You can draw your own circle and do it, but be sure you start with the circle and point A and then construct the tangents and not in the reverse order.)

Problem 5. Consider the figure on page 48 of GTC, Exploration 4.3. A is the center of a circle and points C, D, E are on the circle. State and prove the relationship between the measure of angle CDE and the measure of angle CAE. (Is there more than one angle CAE? Clarify this.)