
NAME .
Instructions. When a problem calls for a CONSTRUCTION, this means a straightedge and compass construction. Write down the main steps of the construction so that a reader can easily understand what you did. You do not need to justify your steps.
Imagine the figure below extended over the whole plane to form a wallpaper pattern. For this pattern, mark all the symmetries as follows:
· Mark centers of rotation (fat dots for 180 degrees, squares for 90 degrees, etc.).
· Mark the mirror lines of reflection symmetries with double lines.
· Mark the invariant lines of glide reflections with dashed lines (unless the line is already marked as a double line). Indicate the magnitude of the translation component of the glide reflection by arrows or marks on the dashed line itself.
· Indicate the basic translations t and t' with arrows and shade in one of the parallelograms defined by these translations. (By basic translations we mean translations chosen so all the other translations are products of these or their inverses.)

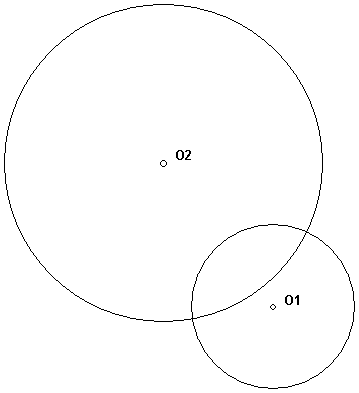
In the figure are two circles with centers O1 and O2 and radii r1 and r2.
· Construct the centers of similitude of these circles.
· Construct all common tangents to the two circles.
In the figure below, let F be dilation with center O and ratio 3/5. Construct the point P' = F(P).

Given a right triangle ABC with right angle at A and side lengths a = |BC|, b = |CA|, c = |AB|, let D be the foot of the altitude through A.
(1) Find the length |BD| in terms of a, b, and c.
(2) Find the length |DC| in terms of a, b, and c.
(3) Show how to derive the Pythagorean theorem by adding the results of (1) and (2) to get |BC|.
(a) Let ABCD be a quadrilateral. Form a new quadrilateral EFGH whose vertices are the midpoints of the sides of ABCD. EFGH has a special shape. State what this shape is and prove it.
(b) True or False? The midpoint quadrilateral of an isosceles trapezoid is a rhombus. Give a short but convincing explanation for your answer.
(a) State the definition of glide reflection.
(b) We call the special line used to define a glide reflection its invariant line. Prove this: If G is a glide reflection and P is any point not on the invariant line of G, then the midpoint M of PP' is on the invariant line of G, where P' = G(P).
Given A and B in the figure, let F = rotation with center A by 180 degrees and G = rotation with center B by 60 degrees.
(a) What kind of isometry is the composition H = FG?
(b) Construct in the figure the defining data of H so that we know precisely what H is (special points or lines, angles, etc.).
![]()
Let ABCD be a kite (with |AB| = |AD| and |CB| = |CD|). Which of the following is true? Circle your answer.
(i) For any kite ABCD, there is a circle that passes through A, B, C and D.
(ii) For no kites ABCD, there is a circle that passes through A, B, C and D.
(iii) For some kites ABCD, there is a circle that passes through A, B, C and D.
If (i) or (ii) is true, justify your answer. If (iii) is true, describe all the kites for which there is such a circle and justify your answer. Note: This is an "if and only if".
A hexagon ABCDEF is called a parhexagon if the opposite sides are parallel and equal in length, i. e.
· AB and DE are congruent and parallel.
· BC and EF are congruent and parallel.
· CD and FA are congruent and parallel.
Prove that the three diagonal segments AD, BE, and CF are concurrent.
Please do not write in this table. It is for the grader.
|
Problem (with score possible) |
Score |
|
1 (25 points) |
|
|
2 (25 points) |
|
|
3 (15 points) |
|
|
4 (20 points) |
|
|
5 (25 points) |
|
|
6 (25 points) |
|
|
7 (25 points) |
|
|
8 (25 points) |
|
|
9 (25 points) |
|
|
TOTAL (210 possible) |