Exterior angle theorem
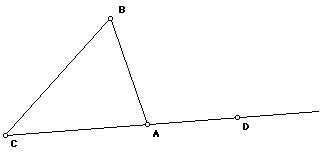
Let ABC be a triangle and let D be a point on line AC so that A is between C and D. Thus angle BAD is an exterior angle of the triangle at A.

Use the angle sum theorem and supplementary angles to write an equation relating the measures of angle B, angle C and angle BAD.
In the special case that triangle ABC is isosceles, with AB = AC, this equation can be simplified to an equation relating angle C to angle BAD. What is this equation?
Exterior angle inequality
One consequence of the Exterior Angle Theorem is a relation of inequality as well. For example, what inequality relates these angles?
angle C _____ angle BAD
angle B _____ angle BAD
This can be expressed in words: In a triangle, an exterior angle is supplementary to the adjacent interior angle and is greater than either of the non-adjacent interior angles.
Angles in Right Triangles
Let ABC be a right triangle with right angle A and angle B = b and angle C = c. Let O be the midpoint of the hypotenuse BC. Then the segment OA divides the right triangle into two isosceles sub-triangles.
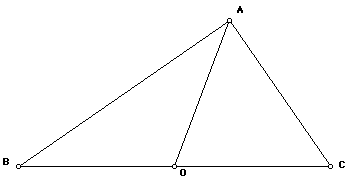
Why are the sub-triangles isosceles? (Give a good, convincing answer, if not a formal proof.)
In the figure, mark by each angle its measure, written as an expression in b and c.
Also write the missing part of the equations.
angle ABC = angle AOC
angle ACB = angle AOB
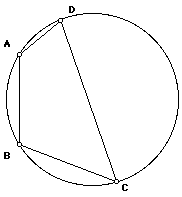
Measuring Arcs
Given a circle with center O and two points P and Q on the circle, the rays OP and OQ define angle POQ. An angle with vertex at the center of the circle is called a central angle of the circle. The points P and Q divide the circle into two arcs. If chord PQ is a diameter, both arcs are semicircles. Otherwise, the angle is less than 180 degrees and the arc lying inside the angle is called the minor arc PQ. Its measure, or arc angle, is the same as the measure of the central angle POQ. The other arc, consisting of points exterior to angle POQ, is called the major arc PQ. The arc angle measure of the major arc is 360 - measure of angle POQ. The measure of a semicircle is =180 degrees.
Thus for example, if angle POQ = 50 degrees, the minor arc is an arc of 50 degrees and the major arc is an arc of 310 degrees.
Right Triangles and Arcs
As we know from the Carpenter Theorem (OA = OB = OC as explained above), the circle with center O and radius OA is the circumcircle of ABC, with BC a diameter.
Given the same angles as on the previous page, write the measures of the 3 arcs in the figure.

Inscribed Angles
Given a circle, an angle is defined to be an inscribed angle of the circle if the angle = angle PAQ, where A, P and Q are points on the circle. The points on the circle which are interior to an inscribed angle PAQ form an arc. This is called the included arc of the inscribed angle or sometimes simply the arc defined by the inscribed angle.
In the figure on the previous page, there are 3 inscribed angles. What are they?
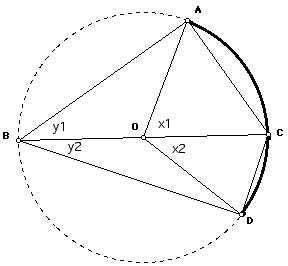
In the figure above, BC is a diagonal. Combining all your work so far, write one equations relating x1 = angle AOC to y1 = angle ABC and one equation relating x2 = angle COD to y2 = angle CBD.
But angle ABD = y1 + y2. Write an equation that relates angle ABD to angle AOD.
Moving the point B
The figure below has exactly the same circle as before and the same points A and B, but the diameter B'C' has replaced BC.
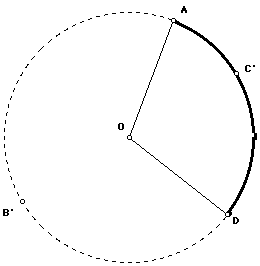
Fill in any segments you need and repeat the previous exercise to find an equation relating angle AOD and angle AB'D. First use the right triangles AB'C' and DB'C' to write equations relating angle A. Fill in the blanks in these equations.
angle AB'C' = angle AOC'
angle C'B'D = angle C'OD
Adding the angles on the left side and the angles on the right side we get another equation.
angle AB'D = angle AOD
Overlapping case
In the figure below, there the points A and D are still the same, and B'C' is still a diameter, so the triangles AB'C' and DB'C' are still right triangles.
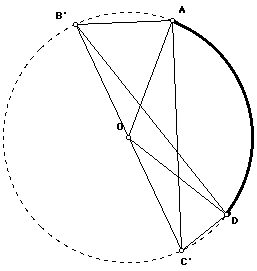
Work with these triangles to find relations as before and check whether the same equations still hold.
angle AB'C' = angle AOC'
angle C'B'D = angle C'OD
Subtracting one equation from the other, we get another equation.
angle AB'D = angle AOD
Inscribed Angle Theorem.
If ABC is an inscribed angle, the measure of ABC is one-half the measure of its included arc.
Application 1
In this figure, mark the equal angles and find some similar triangles. Write some equal ratios or products resulting from the similar triangles.
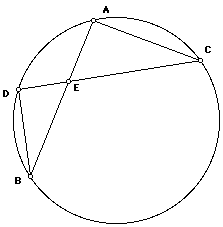
Application 2
If a quadrilateral ABCD is inscribed in a circle, the angles BAD and DCB are both inscribed angles with the same end points. What is the relationship between these angles? What is the relationship between the angles at vertices B and D?