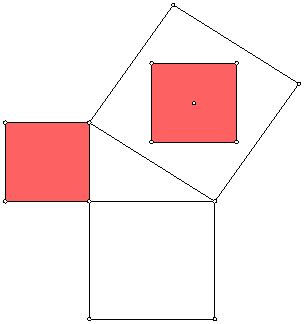
Assignment 10C (Due Monday 12/4, 35 points + 10 extra)

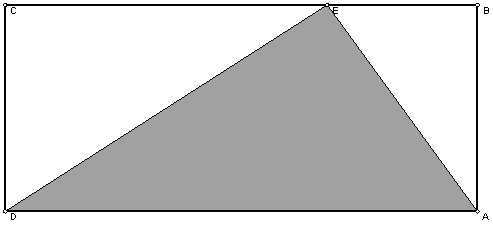
10.7 Reasembling Rectangles #1 (10 points)
  1. In the figure below, a rectangle is cut up into 3 triangles. Cut out the shape (or a copy of it) and assemble from the pieces a rectangle with one side = AE.

  2. Construct a rectangle of different dimensions and construct (and explain how to construct) a point E so that angle AED is a right angle and the rectangle can be divided as in (a). Also, if this construction is sometimes impossible, explain when it does not work.

    3. 10.8 Reasembling Rectangles #2 (10 points)
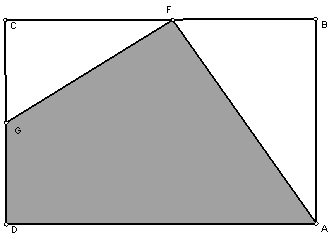
  3. In the figure below, a rectangle is cut up into2 triangles and a quadrilateral. Cut out the shape (or a copy of it) and assemble from the pieces a rectangle with one side = AE. You may have to cut one or more triangles. What shape does this new rectangle appear to be? Can you believe your eyes (remember the area puzzle from Wednesday).

  4. In the figure above, if AB =a and BC = b, what length must AF be in order for the reassembled rectangle with side AF to be a square. If you are given a and b, how to you construct this length? Show this construction in an example of your own.

 

10.9 Rectangle Angle Bisectors (10 points)
  1. Prove that the interior angle bisectors of a rectangle ABCD intersect in four points EFGH that are the vertices of a square.
  2. Tell what are the symmetries of EFGH. Can you use the symmetries to prove part (a)?
  3. What figure do the exterior angle bisectors form?

 

10.10 Areas in a parallelogram (5 points)

Given a parallelogram ABCD. If E is a point on the diagonal BD, the lines through E parallel to the sides cut the parallelogram into 4 small parallelograms. Prove that two of these 4 parallelograms, the ones with vertices at A and E, have the same area.

 

 

Extra Credit (10 points)

We discovered in class, that a puzzle formed in this manner, from a big square and a smaller central square, does not always fit together into two squares.

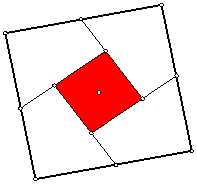
Construct a square-within square puzzle that can be rearranged to be two squares, following the positioning of the central square from the figure below. This is actually the figure for a Chinese proof of the Pythagorean theorem, done independently from Western geometry.