Reading. If you have not done so, complete your reading of Chapter 5. Also it would be a good time to review the constructions in Chapter 6. We have done almost all of them, either in homework or in lab. Also, read B&B Chapter 9 on Loci. You will discover that in lab and in class and homework, we have proved Locus Theorems 1 – 6 and Locus Theorem 7 will be proved this week. The use of the locus concept in construction is a very powerful one. Also, bear in mind as you think towards the midterm test that the problems and theorems of the course are not only the problems of the assignments, but the problems done as class activities and in labs. There will be some review information forthcoming soon, but your own notes a most important resource.

Draw a segment AB on a page. Let s be the length AB. The construction problem is to construct with straightedge and compass a regular pentagon ABCDE with one side being the given AB. In the interest of being comprehensible, please label important points and write out briefly the major steps of your construction so that it is easy to understand what you did. You do not have to prove that your method works.

Here is one suggestion for doing this construction.

1. Construct with straightedge and compass a segment of length d = (1 + sqrt(5))s/2.
2. Use the two distances given to construct triangles by SSS. Each triangle can have two vertices being A and B and the other being C, D or E.

Remark: There is a construction for the regular pentagon given in B&B, but the construction there is not an answer to this question, since that construction takes as given the center O of the pentagon and one vertex A. It is simpler to use the class handout from Monday 10/23 as a guide.

Let ABCD be a rectangle, with AB < BC. Then there is a point E on segment AD and a point F on segment BC such that CDEF is a square and BFEA is a rectangle. We say that ABCD is a golden rectangle if BFEA is similar to ABCD. If ABCD is a golden rectangle, there is only one possible ratio BC/AB. Compute this number (exactly). Give your reasoning.

Given a triangle ABC, for each vertex, construct the line through the vertex parallel to the opposite side. Thus line a is the line through A parallel to BC, line b is the line through B parallel to CA, and line c is the line through C parallel to AB. The three lines a, b, c define a new triangle A'B'C', with vertices A' = intersection of b and c, B' = intersection of c and a, C' = intersection of a and b.

• Prove that ABC is the midpoint triangle of A'B'C'.
• Conclude that the altitude lines of ABC are the perpendicular bisectors of the sides of A'B'C'.
• Use a fact that we know about perpendicular bisectors to prove that the altitude lines of any triangle ABC are concurrent.

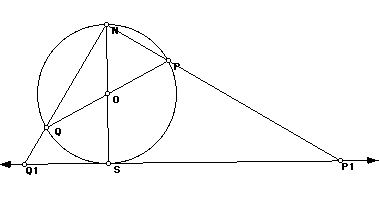
In the figure, the circle has center O and radius r. PQ and NS are diameters. Line P1 Q1 is tangent to the circle at S.

(N, P and P1 are collinear and also N, Q, Q1 are collinear, as they appear to be.) Problem: Find a relationship among the quantities |NS|, |SP1|, |SQ1|.

Given an isosceles triangle ABC, with |AB| = |AC| = b and |BC| = a, what is the radius R of the circumcircle of ABC? (The answer should be in terms of a and b, if possible.)

Note: There are cases that you may need to consider separately, namely the case when P is outside the circle and the case when P is inside the circle (the case when P is on the circle is easy). This is the same as B&B problems 35 and 36 on page 151. Check that page for figures and hints.