Given a triangle ABC, let A' be the foot of the altitude through A, B' be the foot of the altitude through B and C' be the foot of the altitude through C. Prove that AA'*BC = BB'*CA = CC'*AB.

(Note: The foot of the altitude may lie on the side extended. For example, A' is the intersection of line BC with the line through A perpendicular to BC. If B or C is obtuse, A' will not lie on segment BC.)

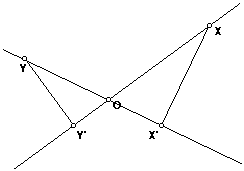
First we will prove a general relation. Let m and n be two lines intersecting at O which are not perpendicular. Then the lines form four angles at O. Two are equal to an acute angle a, and the other two are obtuse and equal 180 - a.

Let X be a point on line m, distinct from O, and let X' be the intersection of m with the line through X perpendicular to m. Then triangle OXX' is a right triangle with right angle OX'X, so by angle sum the other two angles OXX' and XOX' are acute. Therefore, angle XOX" must equal a and not 180 - a.

Now let Y be another point on one of the lines and let Y' be the foot of the perpendicular from Y to the other line. By the same reasoning, OYY' is a right triangle, with angle YOY' = a. Then by AA, triangle OXX' is similar to triangle OYY'. From this it follows that XX'/YY' = OX/OY, or XX'*OY = YY'*OX.

Now this can be applied to prove the theorem. Given triangle ABC, at least two of the angles are acute. Label the triangle so that angle A and angle B are acute angles.

The lines AB and AC are lines intersecting at A. Applying the reasoning above, letting A be O, B be X and C be Y, triangle ABB' is similar to ACC', so BB'*CA = CC'*BA.

Now consider the lines BA and BC intersecting at B. The same reasoning gives AA'*CB = CC'*AB. Combining these two results completes the proof. QED

Notice that the result was proven even for right triangles by only considering two vertices with acute angles. However, the right triangle case is interesting and should be discussed. If angle C is a right angle, then A' = C and also B' = C, so the result becomes AC*BC = BC*CA = CC'*AB, or just the product of the lengths of the legs = CC'AB.