How to get a rotation as a product formed from two other rotations

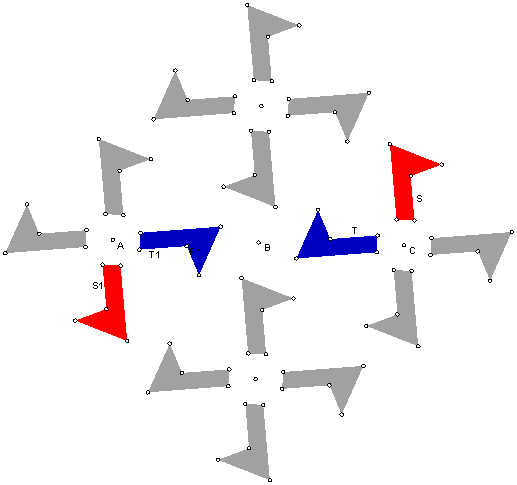
Suppose we are given two points A and B and a shape Z. Let A₉₀ be rotation by 90 degrees with center A and B₉₀ be rotation by 90 degrees with center B. Then we can generate a symmetric pattern on the whole plane by applying A₉₀ and B₉₀ to Z and the images of Z. In effect we are looking at all shapes Z', where Z' is obtained from Z by an isometry which is a product of powers of A₉₀ and B₉₀. We have done this in lab and the pattern might start out something like this. Two pairs of shapes are colored in a special way to answer the question below.

We see that in this figure the shape T is obtained from shape S by C₉₀, the rotation by 90 degrees with center C. So it must be possible to write C₉₀ as a product made up only of A₉₀ and B₉₀. How can we tell what this is?

Notice that by a point symmetry in B there are shapes S1 and T1, with T1 = A₉₀(S1). But S1 = B₁₈₀(S) = (B₉₀)²(S) and likewise T1 = B₁₈₀(T) and T = B₁₈₀(T1).

Putting this together, we see that we can get from S to T as a chain of isometries which take S ->S1->T1->T and this chain can be written in functional notation as T = B₁₈₀(T1) = B₁₈₀(A₉₀(S1)) = B₁₈₀(A₉₀(B₁₈₀(S))). So we have T = F(S), where F = B₉₀² A₉₀ B₉₀².

Since two isometries that agree on 3 noncollinear points are the same isometry, and since T = C₉₀(S), then C₉₀ = F.