Sec 3.3, Problem 20

Let A be the matrix with columns v, w, so 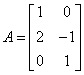. We are asked whether a certain vector b is in Sp(S), where S is the set {v,w}. In other words, is b in the range of A? This is the same as asking whether the equation Ax = b can be solved. This equation is the same as x₁v + x₂w = b.

So we can either solve each problem separately, or we can get a formula by letting .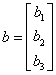

Then reducing the augmented matrix yields this:

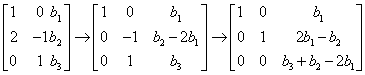
Thus a vector b is in the span if . If this equation is satisfied, then x₁v + x₂w = b where x₁ = b₁ and x₂ = b₁ – b₂.

So the answers are

(a) 1 + 1 – 2 = 0, so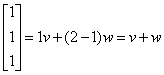

(b) -1 + 1 – 2 is not 0, so not in span.

(c) 0 + 2 - 2 = 0. We can use the formula, or we can just notice that this vector = v (thus = 1v + 0w).

(d) 1+3 – 4 = 0, so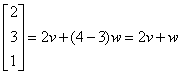

Section 3.4, Problem 6

The coefficient matrix of this homogeneous system is A = 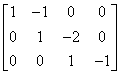. To find a basis of W, solve the equation Ax = 0. The solutions are all multiples of so this vector is a basis for W. (Thus W is a line through 0, a 1-dimentional subspace.)

Section 3.4, Problem 8

The coefficient matrix of this homogeneous system is A = , which reduces to . The solution set of Ax = 0 is the set of X of the form

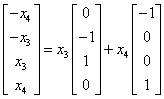. Thus a basis of W is .

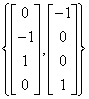S does not span because a set of two vectors cannot span all of 3-space. A vector b is in the span of S if we can solve the equation Ax = b, where the columns of A are the vectors in S. In other words, we are asking if b is in the range of A.

Section 3.4, Problem 12

(a) The matrix A reduces thus: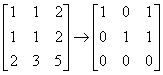

(b) Null space is the set of all X = 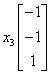so 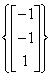is a basis of N(A).

(c) Since .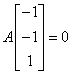

If the columns of A are A₁, A₂, A₃, this says (-1) A₁ + (-1) A₂ + A₃ = 0 or

A₃ = A₁ + A₂. So we get the same set of all linear combinations (span) if we remove A₃ from the set. But { A₁, A₂}, so we stop here. This set is a basis of the column space.

(d) Basis for the row space is {[1 0 1], [0 1 1]}.

For details, see examples in this section and notes from Wed 10/25.

Section 3.4, Problem 14

(a) This matrix reduces to the 3x3 identity matrix I.

(b) The null space N(A) = the zero subspace = {0}. One can either say the zero subspace has no basis (see p. 195 after Def 4) or adopt the slick convention that a basis is the empty set {}. Either one is OK in this course, for now at least.

(c) A basis for the column space (range) consists of the set of all 3 columns of A.

(d) A basis for the row space could either be the rows of A or else the rows of I. (the standard basis of R³).

Supplementary Problems, page 266, Problem 3

This equation Ax = 3x, if written out is a linear system in x1, x2, x3 with variables on both sides of the equation. Move all the variables to the left side and get a new matrix. This matrix is actually A – 3I. Call this matrix B

(a) This is N(B), thus a subspace.

(b) Find a basis of N(B) as in problems above and in examples

The reduce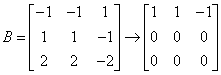

Vectors in null space of B are solutions of Bx = 0. This is set of these linear combinations: 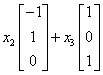. Thus a basis of N(B) = .

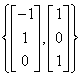Since the basis has two elements, the dimension = 2.

Common sense note: Once we set up the matrix B, we see that the 3 equations are multiples of one equation in the 3 variables. Thus the solution is a plane, which has dimension 2.