December 17, 2009
Stats on the final exam: min=46; median =81; max=100 (1 student).
The grade record has been updated with the latest writing problem scores and final exam scores. I will be adding course grades some time today or tomorrow.
December 12, 2009
Grading of the final has commenced. I will update the Catalyst grade book with scores and course grades once I have them. I will hold an office hour on Friday, from 1 PM to 2 PM, if you would like to stop by to see your final exam. I'll have your exam next quarter, too, if you would like to see it then.
Have a good break!
December 6, 2009
Here is a review sheet for the final exam.
December 4, 2009
Here are some thoughts on the latest writing problem.
- The inequality |(x-sin x)/x3| ≤ 1/6 makes no sense if x=0. So consider instead the nearly equivalent |x-sin x| ≤ 1/6 |x|3.
-
There are places in the arguments you need to make in this problem where you ought to use either -1 ≤ sin x ≤ 1 or -1 ≤ cos x ≤ 1. These facts can be used very effectively to make conclusions about, for instance, the sign of a derivative.
-
For example, suppose we wanted to show that sin2x-3x ≤ 0 for all x ≥ 0. We can let f(x)=sin2x-3x and study this function.
We find f'(x)=2 sin x cos x - 3.
Since -1 ≤ sin x ≤ 1 and -1 ≤ cos x ≤ 1, we know sin x cos x &le 1.
Hence, f'(x) ≤ 2-3 = -1 < 0;.
Thus f(x) is always decreasing.
Since f(0)=0, we may conclude that f(x)<0 for x>0.
In other words, sin2x-3x ≤ 0 for all x ≥ 0.
December 4, 2009
I was a little rushed at the end of today's lecture.
In the cone-inside-a-sphere example, we worked out that the
optimal height of the cone is 4/3 R, where R is the radius
of the sphere. This gives a optimal radius for the cone of
r=sqrt(8)/3 R.
The maximum possible volume is then 32/(81 Pi) R3, which
is exactly 8/27 the volume of the sphere.
We might imagine that the optimal cone would have a nice geometric property. For instance, we might guess that the optimal cone would look like an equilateral triangle when viewed in profile (as in the sketch we made for solve the problem). However, with the optimal height and radius we found we see that the angle the sloping side makes with the base of the cone has a tangent of sqrt(8), which is greater than the tangent of 60 degrees, which is sqrt(3). The arctangent of sqrt(8) works out to 70.52877.. degrees, so the optimal cone has a profile which is a steeper than an equilateral triangle.
December 3, 2009
Gradebook scores are now available via MyUW and Catalyst tools. Please check that all of your scores have been recorded correctly. If you find an error, please bring the exam or homework to me or Lee so we can correct the error.
Included with your scores is a "Total Score". This a percentage score, with 100 representing absolute perfect performance, and 0 is nothing was turned it at all. An estimate of your current grade situation can be attained by using the formula
estimated grade = 0.054637 (Total Score) - 1.0.So, for instance, if your Total Score is 82 percent then the esimated grade would be 0.054637(82)-1.0=3.477.
This is a very rough estimate, and sets the median grade in the course a little lower than what I expect it will be. Also, at the lower end of the scale, it may be an overestimate, as I am working under the assumption that everyone should pass on to Math 125. A lot depends on the final exam, and I may change that assumption based on final exam performance.
In general, it's probably reasonable to think of this estimate with a plus or minus 0.2 window of error. So, for instance, an 82 would mean something between 3.277 and 3.677.
In addition to the final, there is also the third writing problem. I'm hoping everyone does well on this, and that will help narrow the current range of Total Scores, and that will mean higher grades for those at the lower end of things.
December 2, 2009
There was a problem with the way I stated the third part of the latest writing problem. Please take a look at this thread on the class discussion board for a correction.
December 1, 2009
Answers to the second midterm exam are now in the archive.
November 30, 2009
As mentioned in class today, I removed section 4.7 from the homework schedule since I spent the entire lecture today discussing writing problems. We will talk about 4.7 material on Friday, and you should do the assigned 4.7 problems well in advance of the final.
November 27, 2009
Here are the stats for the second midterm exam: n=57; min=27; 1st quartile=50; median=56; 3rd quartile=62; max=70 (2 students)
I'll be making your grade record available to you in the next week or so. This is so you can check that your exam and homework scores have been recorded correctly. At that time, I will also give you an estimated course grade which will take into account all of your scores so far.
November 19, 2009
Here is a review sheet for the second midterm coming up on Tuesday, November 24.
In addition to what is listed on the review sheet, you should also be comfortable with applying calculus to curves defined parametrically and using calculus to investigate parametric motion. Pay close attention to the assigned homework, especially the non-textbook problems on this topic.
November 13, 2009
The worksheet for Tuesday is here. This expands on last week's worksheet, filling out the method of Newton's Method. There are a few Newton's Method problems on this week's homework assignment, taken from section 4.8. Newton's Method problems make nice exam questions.
November 9, 2009
In discussions with a few students, it has been made clear to me that for the analysis of dy/dx and tangent lines to the curve in the writing problem, the cartesian equation is much easier to work with. There are some technicalities involved when studying dy/dx for this curve at the point of self-crossing (as it is called), and the cartesian form makes this quite a bit simpler. So, I strongly recommend that you study dy/dx via the cartesian equation rather than via the parametric equations.
Also, I am aware that there is considerable material related to this curve on the web, including material provided by the publishers of our text. I would like to point out a couple of things. First, a lot of this information is, at best, incomplete, and at worst, incorrect, so consider what you read with a great deal of caution. Second, be sure that your work on the writing problem is yours, and yours alone: be careful not to plagiarize.
November 9, 2009
Writing Problem 2 is now due next Monday, November 16 (instead of this Friday, November 13). Many people spoke to me today and showed lots of good effort toward solutions to the problem.
November 3, 2009
Here is a little writeup on finding lines simultaneously tangent to two curves.
November 2, 2009
I have updated the solutions to midterm exam 1. There were changes to problem 1(b) and problem 3.
November 1, 2009
Writing Problem 2: The Folium of Descartes is a curve defined
parametrically by the equations
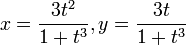
Thoroughly analyze this curve.
Find all symmetries and asymptotes. Find all vertical and horizontal tangent lines.
Give a cartesian equation for the curve. Determine the "extreme" points of the
loop. Sketch the curve.
November 1, 2009
Here is an applet illustrating an idea related to problem 3 from the midterm.
October 30, 2009
Answers to the midterm are now available in the archive (link at right).
October 30, 2009
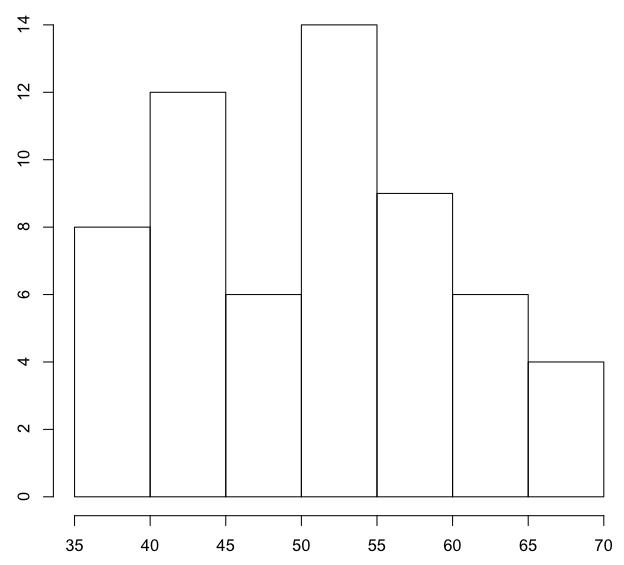
Some stats on the first midterm:
n=58; min=36; 1st quartile=44; median=52;
3rd quartile=57.5; max=68 (2 people).
Here's a histogram of the exam scores:
October 24, 2009
I just realized that the review sheet I posted contains a mistake in that it does not mention that section 2.4 is also relevant for this midterm. So please pay attention to those problems assigned for that section.
October 23, 2009
My exam archive (link at right) is a good source for old exam problems to practice with. Even though only the first two (Autumn 2007 and 2008) are honors sections, the other problems have at least some problems very much worth considering before the midterm. On Monday in lecture, we can discuss any questions you have about any of these exams, or anything else.
October 22, 2009
Here is a review sheet for the first midterm. Also, the homework schedule has been augmented to include a few problems from 3.2 and 3.3.
October 21, 2009
Here is an applet I just wrote to illustrate the idea that normals to the graph of a quadratic function y=x2 miss some of the y-axis.
Note that your browser will need to have Java enabled for this to work.
October 11, 2009
Here is an animation related to an example from Monday's lecture.
Also, please bring this worksheet to quiz section on Tuesday. If you have the course pack, you have it already.
October 5, 2009
Please print out this worksheet and bring it to quiz section tomorrow (Tuesday). If you have the course pack, you already have the worksheet.
October 4, 2009
Here are some suggestions for the first writing problem. Be sure to also check out the examples on the discussion board.
October 1, 2009
I have added some writing problem examples to the discussion board (link at right). Do take a look.
October 1, 2009
Everyone should know that the homework assignment is found via the link on the right side of this page. Click on that link, and you will find the homework assignment for next Friday. I'll be adding more problems later today.
That page is the only way to know what the homework assignment is. I assign problems different from those assigned to the non-honors sections of 124.
September 28, 2009
About the course textbook:
The textbook for the course is Calculus, by Stewart, 6th edition, early transcendentals version. The full (i.e. standard) textbook will cover the courses Math 124, 125 and 126, as well as Math 324. It's probably available used from various sources.
The bookstore has custom printed (paperback) versions of the text: one covers 124 and 125, the other 126. As far as I know, they are not selling used copies of this.
Read about the optional course pack below.
September 21, 2009
About the 124 Course Pack: At the UW bookstore (as of 9/21), you can purchase a collection of printed items known as the "124 Course Pack". This contains all of the worksheets you will need for the course, plus other supplementary materials like old exams. All of the material in the course pack is available on the 124 Materials Website (link at right), so you welcome to just print things out as you need them. The course pack is available for your convenience.
September 20, 2009
Welcome to Math 124 K, Autumn quarter 2009.
Announcements and other useful things will be posted here during the quarter, so check this site frequently.